Bac 2021 (8 juin 2021): étude de fonction avec exponentielle
Exercice corrigé - Spécialité maths, terminale générale
Partie 1
On donne ci-dessous, dans le plan rapporté à un repère orthonormé, la courbe représentant la fonction dérivée
À l'aide de cette courbe, conjecturer, en justifiant les réponses :
- Le sens de variation de la fonction
 sur
sur  .
.
- La convexité de la fonction
 sur
sur  .
.
(4,4.5)
\psaxes[linewidth=1.25pt](0,0)(-2,-1.25)(4,4.5)
\psaxes[linewidth=1.25pt]{->}(0,0)(1,1)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=red]{-2}{4}{1 x add 2.71828 x exp div neg}
\rput(1,-1.5){Courbe repr\'esentant la \textbf{d\'eriv\'ee} $f'$ de la fonction $f$.}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021/8.png)
Partie 2
On admet que la fonction
On note
On admet que la fonction
- Montrer que, pour tout nombre réel
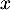 ,
,
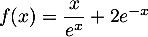 .
.
En déduire la limite de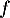 en
en 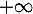 .
.
Justifier que la courbe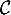 admet une asymptote que l'on précisera.
admet une asymptote que l'on précisera.
On admet que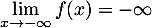 .
.
-
- Montrer que, pour tout nombre réel
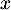 ,
,  .
.
- Étudier les variations sur
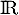 de la fonction
de la fonction 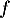 et dresser son tableau de variations.
et dresser son tableau de variations.
- Montrer que l'équation
 admet une unique solution
admet une unique solution 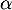 sur l'intervalle
sur l'intervalle ![$[-2~;~-1]$](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021/32.png) dont on donnera une valeur approchée
à
dont on donnera une valeur approchée
à 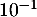 près.
près.
- Montrer que, pour tout nombre réel
- Déterminer, pour tout nombre réel
 , l'expression de
, l'expression de 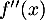 et étudier la convexité de la fonction
et étudier la convexité de la fonction  .
.
Que représente pour la courbe son point A d'abscisse
son point A d'abscisse  ?
?
Correction
Baccalauréat général, spécialité mathématiques, Métropole 8 juin 2021
On admet que la fonction mentionnée dans la Partie 1
est définie sur
mentionnée dans la Partie 1
est définie sur  par:
par: 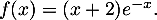
Cacher la correction
Baccalauréat général, spécialité mathématiques, Métropole 8 juin 2021
Partie 1
- D'après la courbe représentant la fonction dérivée
 :
:
- la fonction
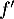 est positive sur
est positive sur ![$]-\infty~;~1[$](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021_c/3.png) donc la fonction
donc la fonction  est croissante sur cet intervalle;
est croissante sur cet intervalle;
- la fonction
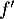 est négative sur
est négative sur ![$]1~;~+\infty[$](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021_c/6.png) donc la fonction
donc la fonction 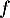 est décroissante sur cet intervalle.
est décroissante sur cet intervalle.
- la fonction
- D'après la courbe représentant la fonction dérivée
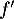 :
:
- la fonction
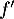 est décroissante sur
est décroissante sur ![$]-\infty~;~0[$](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021_c/10.png) donc la fonction
donc la fonction 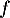 est concave sur cet intervalle;
est concave sur cet intervalle;
- la fonction
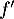 est croissante sur
est croissante sur ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021_c/13.png) donc la fonction
donc la fonction 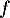 est convexe sur cet intervalle.
est convexe sur cet intervalle.
- la fonction
Partie 2
On admet que la fonction
- Pour tout nombre réel
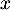 ,
,
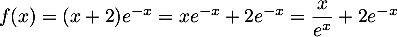 .
.
Par croissances comparées on a: donc
donc  .
.
De plus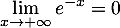 donc
donc 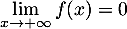 .
.
On en déduit que la courbe admet la droite d'équation
admet la droite d'équation 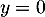 ,
c'est-à-dire l'axe des abscisses, comme asymptote horizontale en
,
c'est-à-dire l'axe des abscisses, comme asymptote horizontale en 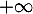 .
.
-
-
 .
.
- Pour tout
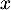 ,
, 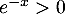 donc
donc 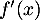 est du signe de
est du signe de  ;
donc
;
donc 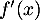 s'annule et change de signe en
s'annule et change de signe en 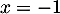 .
.
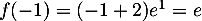 ;
on établit le tableau de variations de
;
on établit le tableau de variations de 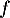 sur
sur 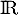 :
:
![\[{\renewcommand{\arraystretch}{1.5}
\psset{nodesep=1pt,arrowsize=5pt 3}
\def\esp{\hspace*{2.5cm}}
\def\hauteur{0pt}
\begin{array}{|c|l*4{c}|}
\hline
x & -\infty & \esp & -1 & \esp & +\infty \\
\hline
-x-1 & & + & \vline\hspace{-2.7pt}0 & - & \\
\hline
f'(x) & & + & \vline\hspace{-2.7pt}0 & - & \\
\hline
& & & \Rnode{max}{e} & & \rule{0pt}{\hauteur} \\
f(x) & & & & & \rule{0pt}{\hauteur} \\
& \Rnode{min1}{-\infty} & & & & \Rnode{min2}{0} \rule{0pt}{\hauteur}
\ncline{->}{min1}{max}
\ncline{->}{max}{min2}
\\
\hline
\end{array}}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021_c/37.png)
- Sur l'intervalle
![$[-2~;~-1]$](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021_c/38.png) , la fonction
, la fonction  est strictement croissante
et continue car dérivable sur cetintervalle.
est strictement croissante
et continue car dérivable sur cetintervalle. 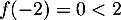 et
et 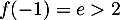 donc,
d'après le corollaire du théorème des valeurs intermédiaires
(ou théorème de la bijection),
l'équation
donc,
d'après le corollaire du théorème des valeurs intermédiaires
(ou théorème de la bijection),
l'équation 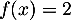 admet une solution unique sur l'intervalle
admet une solution unique sur l'intervalle ![$[-2~;~-1]$](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021_c/43.png) .
.
Avec la calculatrice, on trouve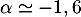 .
.
-
-
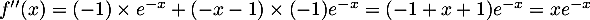
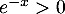 pour tout
pour tout 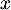 , donc
, donc 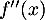 est du signe de
est du signe de 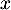 .
.
- Sur
![$]-\infty~;~0[$](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021_c/50.png) ,
, 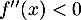 donc la fonction
donc la fonction 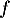 est concave.
est concave.
- Sur
![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021_c/53.png) ,
, 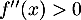 donc la fonction
donc la fonction 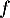 est convexe.
est convexe.
- En
 , la dérivée seconde s'annule et change de signe donc le point A d'abscisse 0 de
, la dérivée seconde s'annule et change de signe donc le point A d'abscisse 0 de  est le point d'inflexion de cette courbe.
est le point d'inflexion de cette courbe.
- Sur
Cacher la correction
Tag:Exponentielle
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
Bac blanc: QCM: fonctions, convexité, suite et programme Python - Probabilités: test pour détecter une maladie - Suites: un peu sur les suites - Géométrie dans l'espace - Fonction logarithme
logarithme népérien: résolution d'équations, étude de fonction, et convexité, points d'inflexion
maison: calculs de dérivées, limites, fonctions et suites récurrentes, démonstration par récurrence et théorème des gendarmes
