Bac 2021 (8 juin 2021): étude de fonction avec exponentielle
Exercice corrigé - Spécialité maths, terminale générale
Partie 1
On donne ci-dessous, dans le plan rapporté à un repère orthonormé, la courbe représentant la fonction dérivée
À l'aide de cette courbe, conjecturer, en justifiant les réponses :
- Le sens de variation de la fonction
 sur
sur  .
.
- La convexité de la fonction
 sur
sur  .
.
(4,4.5)
\psaxes[linewidth=1.25pt](0,0)(-2,-1.25)(4,4.5)
\psaxes[linewidth=1.25pt]{->}(0,0)(1,1)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=red]{-2}{4}{1 x add 2.71828 x exp div neg}
\rput(1,-1.5){Courbe repr\'esentant la \textbf{d\'eriv\'ee} $f'$ de la fonction $f$.}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021/8.png)
Partie 2
On admet que la fonction
On note
On admet que la fonction
- Montrer que, pour tout nombre réel
 ,
,
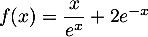 .
.
En déduire la limite de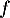 en
en  .
.
Justifier que la courbe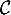 admet une asymptote que l'on précisera.
admet une asymptote que l'on précisera.
On admet que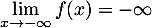 .
.
-
- Montrer que, pour tout nombre réel
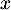 ,
,  .
.
- Étudier les variations sur
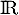 de la fonction
de la fonction 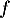 et dresser son tableau de variations.
et dresser son tableau de variations.
- Montrer que l'équation
 admet une unique solution
admet une unique solution 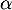 sur l'intervalle
sur l'intervalle ![$[-2~;~-1]$](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021/32.png) dont on donnera une valeur approchée
à
dont on donnera une valeur approchée
à 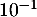 près.
près.
- Montrer que, pour tout nombre réel
- Déterminer, pour tout nombre réel
 , l'expression de
, l'expression de 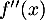 et étudier la convexité de la fonction
et étudier la convexité de la fonction  .
.
Que représente pour la courbe son point A d'abscisse
son point A d'abscisse 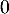 ?
?
Correction
Tag:Exponentielle
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
Bac blanc: QCM: fonctions, convexité, suite et programme Python - Probabilités: test pour détecter une maladie - Suites: un peu sur les suites - Géométrie dans l'espace - Fonction logarithme
logarithme népérien: résolution d'équations, étude de fonction, et convexité, points d'inflexion
maison: calculs de dérivées, limites, fonctions et suites récurrentes, démonstration par récurrence et théorème des gendarmes
