Bac 2019: Suite récurrente (13 septembre 2019)
Exercice corrigé - Spécialité maths, terminale générale
Soit 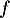 la fonction définie sur l'intervalle [0 ; 4] par
la fonction définie sur l'intervalle [0 ; 4] par
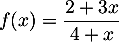 .
.
Partie A On considère la suite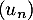 définie par :
définie par :
![\[u_0 = 3 \; \text{et pour tout entier naturel }\; n,\; u_{n+1} = f\left(u_n\right).\]](/Generateur-Devoirs/TS/ChapSuites/ex13092019SR/4.png)
On admet que cette suite est bien définie.
Partie B On considère la suite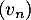 définie par :
définie par :
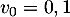 et pour tout entier naturel
et pour tout entier naturel 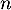 ,
, 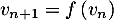 .
.
(0,0)(1.15,1.1)
\psline(1.1,1.1)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{1.15}{3 x mul 2 add x 4 add div}
\uput[d](0.8,0.8){$D$}\uput[u](0.8,0.92){\blue $\mathcal{C}_f$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapSuites/ex13092019SR/32.png)
Correction
Partie A On considère la suite
On admet que cette suite est bien définie.
- Calculer
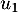 .
.
- Montrer que la fonction
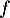 est croissante sur l'intervalle [0 ; 4].
est croissante sur l'intervalle [0 ; 4].
- Montrer que pour tout entier naturel
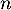 ,
,
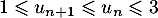 .
.
-
- Montrer que la suite
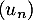 est convergente.
est convergente.
- On appelle
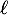 la limite de la suite
la limite de la suite 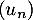 ; montrer l'égalité:
; montrer l'égalité:
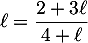 .
.
.
.
- Déterminer la valeur de la limite
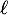 .
.
- Montrer que la suite
Partie B On considère la suite
- On donne en Annexe, à rendre avec la copie, la courbe représentative,
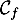 , de la
fonction
, de la
fonction 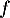 et la droite
et la droite 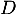 d'équation
d'équation 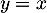 .
.
Placer sur l'axe des abscisses par construction géométrique les termes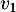 ,
, 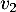 et
et 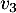 sur
l'annexe, à rendre avec la copie.
sur
l'annexe, à rendre avec la copie.
Quelle conjecture peut-on formuler sur le sens de variation et le comportement de la suite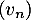 quand
quand 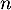 tend vers l'infini ?
tend vers l'infini ?
-
- Montrer que pour tout entier naturel
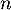 ,
,
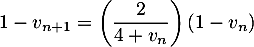 .
.
- Montrer par récurrence que pour tout entier naturel
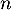 ,
,
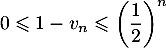 .
.
- Montrer que pour tout entier naturel
- La suite
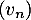 converge-t-elle ? Si oui, préciser sa limite.
converge-t-elle ? Si oui, préciser sa limite.
Annexe
(0,0)(1.15,1.1)
\psline(1.1,1.1)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{1.15}{3 x mul 2 add x 4 add div}
\uput[d](0.8,0.8){$D$}\uput[u](0.8,0.92){\blue $\mathcal{C}_f$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapSuites/ex13092019SR/32.png)
Correction
Tag:Suites
Voir aussi:
Quelques devoirs
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
maison sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, suite auxiliaire arithmétique, convergence monotone et point fixe
