Bac 2019: Suite récurrente (13 septembre 2019)
Exercice corrigé - Spécialité maths, terminale générale
Soit 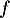 la fonction définie sur l'intervalle [0 ; 4] par
la fonction définie sur l'intervalle [0 ; 4] par
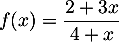 .
.
Partie A On considère la suite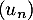 définie par :
définie par :
![\[u_0 = 3 \; \text{et pour tout entier naturel }\; n,\; u_{n+1} = f\left(u_n\right).\]](/Generateur-Devoirs/TS/ChapSuites/ex13092019SR/4.png)
On admet que cette suite est bien définie.
Partie B On considère la suite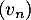 définie par :
définie par :
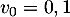 et pour tout entier naturel
et pour tout entier naturel 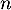 ,
, 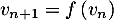 .
.
(0,0)(1.15,1.1)
\psline(1.1,1.1)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{1.15}{3 x mul 2 add x 4 add div}
\uput[d](0.8,0.8){$D$}\uput[u](0.8,0.92){\blue $\mathcal{C}_f$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapSuites/ex13092019SR/32.png)
Partie A On considère la suite
On admet que cette suite est bien définie.
- Calculer
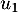 .
.
- Montrer que la fonction
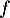 est croissante sur l'intervalle [0 ; 4].
est croissante sur l'intervalle [0 ; 4].
- Montrer que pour tout entier naturel
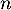 ,
,
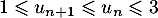 .
.
-
- Montrer que la suite
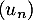 est convergente.
est convergente.
- On appelle
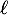 la limite de la suite
la limite de la suite 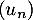 ; montrer l'égalité:
; montrer l'égalité:
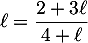 .
.
.
.
- Déterminer la valeur de la limite
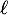 .
.
- Montrer que la suite
Partie B On considère la suite
- On donne en Annexe, à rendre avec la copie, la courbe représentative,
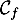 , de la
fonction
, de la
fonction 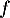 et la droite
et la droite 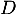 d'équation
d'équation 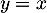 .
.
Placer sur l'axe des abscisses par construction géométrique les termes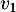 ,
, 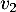 et
et 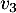 sur
l'annexe, à rendre avec la copie.
sur
l'annexe, à rendre avec la copie.
Quelle conjecture peut-on formuler sur le sens de variation et le comportement de la suite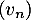 quand
quand 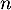 tend vers l'infini ?
tend vers l'infini ?
-
- Montrer que pour tout entier naturel
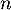 ,
,
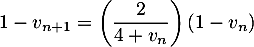 .
.
- Montrer par récurrence que pour tout entier naturel
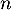 ,
,
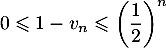 .
.
- Montrer que pour tout entier naturel
- La suite
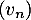 converge-t-elle ? Si oui, préciser sa limite.
converge-t-elle ? Si oui, préciser sa limite.
Annexe
(0,0)(1.15,1.1)
\psline(1.1,1.1)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{1.15}{3 x mul 2 add x 4 add div}
\uput[d](0.8,0.8){$D$}\uput[u](0.8,0.92){\blue $\mathcal{C}_f$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapSuites/ex13092019SR/32.png)
Correction
Partie A
Partie B
Annexe
(0,0)(1.15,1.1)
\psline(1.1,1.1)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{1.15}{3 x mul 2 add x 4 add div}
\uput[ul](1.1,1.1){$D$}\uput[d](1.1,1.03){\blue $\mathcal{C}_f$}
\psline[ArrowInside=->](0.1,0)(0.1,0.561)(0.561,0.561)(0.561,0.8074)(0.8074,0.8074)(0.8074,0.92)(0.92,0.92)
\psline(0.561,0)(0.561,0.561)
\psline(0.8074,0.8074)(0.8074,0)
\psline(0.92,0)(0.92,0.92)
\uput[d](0.1,-0.05){$v_0 =0,1$}\uput[d](0.561,-0.05){$v_1=0,561$}\uput[d](0.8074,-0.05){$v_2=0,807$}\uput[d](0.92,-0.05){$v_3=0,92$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapSuites/ex13092019SR_c/59.png)
Cacher la correction
Partie A
-
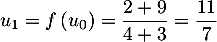 .
.
- La fonction
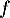 est définie et dérivable sur [0 ; 4] et sur cet intervalle :
est définie et dérivable sur [0 ; 4] et sur cet intervalle :
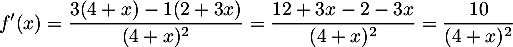
Quotient de nombres positifs ce nombre dérivé est positif quel que soit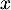 dans l'intervalle [0 ; 4]. La fonction
dans l'intervalle [0 ; 4]. La fonction 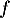 est donc croissante sur [0 ; 4].
est donc croissante sur [0 ; 4].
- Démonstration par récurrence :
Initialisation
On a d'après la première question :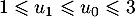 : l'encadrement est vrai au rang
: l'encadrement est vrai au rang 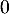 ;
;
Hérédité
Supposons que pour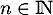 ,
, 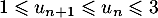 ; par croissance de la fonction
; par croissance de la fonction 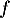 sur [0 ; 4], on
sur [0 ; 4], on
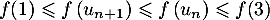 ou car
ou car 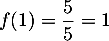 et
et 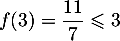 ,
,
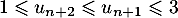 : la relation est donc vraie au rang
: la relation est donc vraie au rang 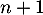 .
.
Conclusion : l'encadrement est vrai au rang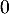 et s'il est vrai à un rang quelconque
et s'il est vrai à un rang quelconque 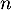 il est vrai au rang suivant
il est vrai au rang suivant 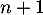 : d'après le principe de récurrence pour tout naturel
: d'après le principe de récurrence pour tout naturel 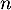 ,
, 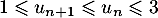 .
.
-
- D'après la question précédente la suite
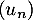 est décroissante, minorée par
est décroissante, minorée par 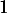 : elle converge donc vers une limite
: elle converge donc vers une limite 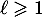 .
.
- De l'égalité
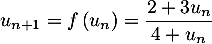 on en déduit par continuité de la fonction
on en déduit par continuité de la fonction 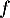 (puisque
(puisque 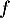 est dérivable) :
est dérivable) :
![\[\ell = \dfrac{2 + 3\ell}{4 + \ell}.\]](/Generateur-Devoirs/TS/ChapSuites/ex13092019SR_c/27.png)
- On en déduit que
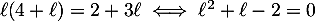 .
.
Or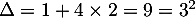 . Il y a deux solutions :
. Il y a deux solutions :
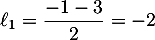 et
et 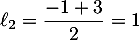 .
.
Comme![$\ell \in [1~;~3]$](/Generateur-Devoirs/TS/ChapSuites/ex13092019SR_c/32.png) , la seule solution est
, la seule solution est 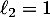 .
.
- D'après la question précédente la suite
Partie B
- Voir l'annexe.
On peut conjecturer que la suite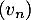 est croissante et qu'elle a pour limite 1.
est croissante et qu'elle a pour limite 1.
-
-
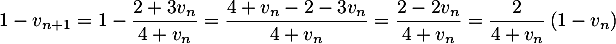 .
.
-
Initialisation pour
 ,
, 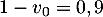 ; or
; or 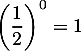 .
On a bien
.
On a bien 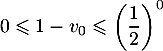 .
.
Hérédité Supposons qu'au rang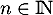 quelconque, on ait
quelconque, on ait 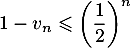 .
.
On a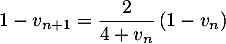 , donc d'après l'hypothèse de récurrence :
, donc d'après l'hypothèse de récurrence :
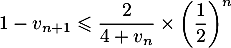 .
.
Or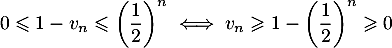 ; il suit que
; il suit que 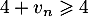 , donc en prenant les inverses
, donc en prenant les inverses 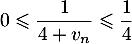 .
.
On a donc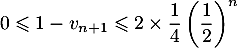 , soit finalement :
, soit finalement :
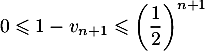 : l'encadrement est vrai au rang
: l'encadrement est vrai au rang 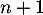 .
.
L'encadrement est vrai au rang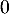 et s'il est vrai à un rang
et s'il est vrai à un rang 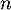 quelconque il est vrai au rang
quelconque il est vrai au rang 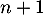 : d'après le principe de récurrence :
: d'après le principe de récurrence :
quel que soit le naturel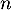 ,
, 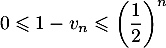 .
.
-
-
Comme
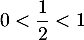 , on sait que
, on sait que  , donc l'encadrement trouvé à la question précédente montre que la la limite de
, donc l'encadrement trouvé à la question précédente montre que la la limite de 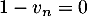 , donc :
, donc :
![\[\dsp\lim_{n \to + \infty} v_n = 1.\]](/Generateur-Devoirs/TS/ChapSuites/ex13092019SR_c/58.png)
Annexe
(0,0)(1.15,1.1)
\psline(1.1,1.1)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{1.15}{3 x mul 2 add x 4 add div}
\uput[ul](1.1,1.1){$D$}\uput[d](1.1,1.03){\blue $\mathcal{C}_f$}
\psline[ArrowInside=->](0.1,0)(0.1,0.561)(0.561,0.561)(0.561,0.8074)(0.8074,0.8074)(0.8074,0.92)(0.92,0.92)
\psline(0.561,0)(0.561,0.561)
\psline(0.8074,0.8074)(0.8074,0)
\psline(0.92,0)(0.92,0.92)
\uput[d](0.1,-0.05){$v_0 =0,1$}\uput[d](0.561,-0.05){$v_1=0,561$}\uput[d](0.8074,-0.05){$v_2=0,807$}\uput[d](0.92,-0.05){$v_3=0,92$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapSuites/ex13092019SR_c/59.png)
Cacher la correction
Tag:Suites
Voir aussi:
