Bac 2013 (Asie) - Un exercice bien complet sur les suites, et avec un algorithme
Exercice corrigé - Spécialité maths, terminale générale
Partie A
On considère la suite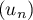 définie par:
définie par: 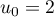 et, pour tout entier naturel
et, pour tout entier naturel 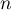 :
:
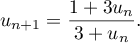
On admet que tous les termes de cette suite sont définis et strictement positifs.
Partie B
On considère la suite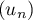 définie par:
définie par: 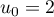 et, pour tout entier naturel
et, pour tout entier naturel 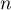 :
:
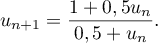
On admet que tous les termes de cette suite sont définis et strictement positifs.
On considère la suite
On admet que tous les termes de cette suite sont définis et strictement positifs.
- Démontrer par récurrence que, pour tout entier naturel
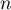 , on a :
, on a : 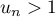 .
.
-
- Établir que, pour tout entier naturel
 , on a:
, on a: 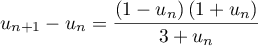 .
.
- Déterminer le sens de variation de la suite
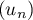 .
.
En déduire que la suite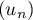 converge.
converge.
- Établir que, pour tout entier naturel
Partie B
On considère la suite
On admet que tous les termes de cette suite sont définis et strictement positifs.
- On considère l'algorithme suivant :

Reproduire et compléter le tableau suivant, en faisant fonctionner cet algorithme pour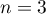 . Les valeurs de
. Les valeurs de 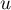 seront arrondies au millième.
seront arrondies au millième.
![\begin{tabular}{|*4{p{1.5cm}|}}\hline
\rule[1.3cm]{0.3cm}{-0.8cm}
$i$&1&2& 3\\ \hline
\rule[1.4cm]{0.3cm}{-0.8cm}
$u$&&&\\ \hline
\end{tabular}](/Generateur-Devoirs/TS/ChapSuites/ex113.Asie/18.png)
- Pour
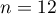 , on a prolongé le tableau précédent et on a obtenu :
, on a prolongé le tableau précédent et on a obtenu :
![\begin{tabular}{|c|*{9}{p{1.3cm}|}}\hline
\rule[1.3cm]{0.3cm}{-0.8cm}
$i$&4&5&6&7&8&9&10&11&12\\ \hline
\rule[1.3cm]{0.3cm}{-0.8cm}
$u$&\footnotesize{1,0083}&\footnotesize{0,9973}&\footnotesize{1,0009}&\footnotesize{0,9997}&\footnotesize{1,0001}&\footnotesize{0,99997}&\footnotesize{1,00001}&\footnotesize{0,999996}&\footnotesize{1,000001}\\ \hline
\end{tabular}](/Generateur-Devoirs/TS/ChapSuites/ex113.Asie/20.png)
Conjecturer le comportement de la suite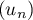 à l'infini.
à l'infini.
- On considère la suite
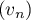 définie, pour tout entier naturel
définie, pour tout entier naturel 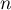 , par :
, par :  .
.
- Démontrer que la suite
 est géométrique de raison
est géométrique de raison  .
.
- Calculer
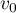 puis écrire
puis écrire 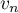 en fonction de
en fonction de 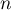 .
.
- Démontrer que la suite
-
- Montrer que, pour tout entier naturel
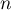 , on a:
, on a: 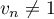 .
.
- montrer que, pour tout entier naturel
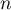 , on a:
, on a: 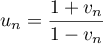 .
.
- Déterminer la limite de la suite
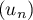 .
.
- Montrer que, pour tout entier naturel
Correction
Partie A
Partie B
Cacher la correction
Partie A
- Initialisation : la relation est vraie au rang
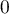 ;
;
Hérédité : supposons qu'il existe un naturel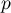 tel que
tel que 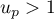 .
.
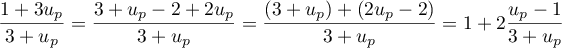 .
.
Par hypothèse de récurrence on a:
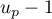 et comme
et comme 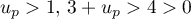 donc son inverse
donc son inverse 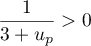 et finalement
et finalement 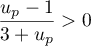 , c'est-à-dire que
, c'est-à-dire que 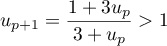
Conclusion: on a démontré, d'après le principe de récurrence, que pour tout entier naturel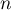 ,
, 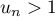 .
.
-
- Pour tout entier naturel
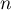 ,
, 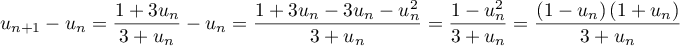 .
.
- On sait que pour tout entier
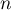 ,
, 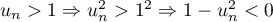 et comme
et comme 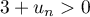 , on a
finalement
, on a
finalement 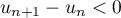 , ce qui signifie que la suite
, ce qui signifie que la suite 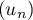 est décroissante.
est décroissante.
La suite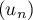 est décroissante et minorée par
est décroissante et minorée par 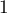 : elle converge donc vers une limite supérieure ou égale à
: elle converge donc vers une limite supérieure ou égale à 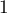 .
.
- Pour tout entier naturel
Partie B
-
![\begin{tabular}{|*{4}{p{1.5cm}|}}\hline
\rule[1.3cm]{0.3cm}{-0.8cm}
$i$&1&2& 3\\ \hline
\rule[1.3cm]{0.3cm}{-0.8cm}
$u$&0,800&1,077&0,976\\ \hline
\end{tabular}](/Generateur-Devoirs/TS/ChapSuites/ex113.Asie_c/22.png)
- La suite semble converger vers
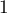 .
.
-
-
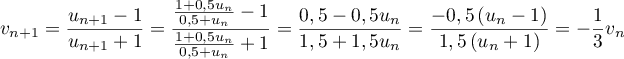 .
.
La suite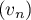 est donc géométrique de raison
est donc géométrique de raison 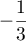 .
.
- On a
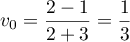 .
.
On sait qu'alors pour tout naturel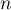 ,
, 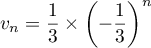 .
.
-
-
- Quel que soit le naturel
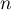 ,
, 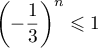 ,
donc
,
donc 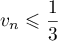 et par conséquent
et par conséquent 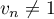 .
.
-
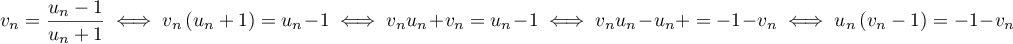 et comme
et comme 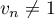 ,
,
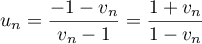 .
.
- Comme
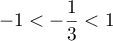 , on sait que
, on sait que 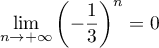 , soit
, soit 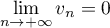 , donc d'après le résultat précédent
, donc d'après le résultat précédent 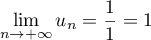 .
.
- Quel que soit le naturel
Cacher la correction
Tag:Suites
Voir aussi:
