Probabilité de maladie de salariés, arbre et loi binomiale, python (d'après Pondichéry)
Exercice corrigé - Spécialité maths, terminale générale
Dans une entreprise, on s'intéresse à la probabilité qu'un salarié
soit absent durant une période d'épidémie de grippe.
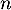 supérieur ou égal à 1, par
supérieur ou égal à 1, par
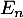 l'évènement « le salarié est absent pour cause de maladie la
l'évènement « le salarié est absent pour cause de maladie la
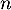 -ième semaine ». On note
-ième semaine ». On note 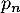 la probabilité de l'évènement
la probabilité de l'évènement
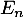 .
On a ainsi:
.
On a ainsi: 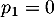 et, pour tout entier naturel
et, pour tout entier naturel 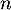 supérieur ou
égal à 1:
supérieur ou
égal à 1: 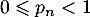 .
.
Correction
- Un salarié malade est absent
- La première semaine de travail, le salarié n'est pas malade.
- Si la semaine
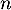 le salarié n'est pas malade, il
tombe malade la semaine
le salarié n'est pas malade, il
tombe malade la semaine 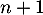 avec une probabilité égale à
avec une probabilité égale à 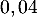 .
.
- Si la semaine
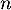 le salarié est malade, il reste
malade la semaine
le salarié est malade, il reste
malade la semaine 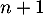 avec une probabilité égale à
avec une probabilité égale à 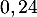 .
.
-
- Déterminer la valeur de
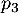 à l'aide d'un arbre de probabilité.
à l'aide d'un arbre de probabilité.
- Sachant que le salarié a été absent pour cause de maladie la troisième semaine, déterminer la probabilité qu'il ait été aussi absent pour cause de maladie la deuxième semaine.
- Déterminer la valeur de
-
- Recopier sur la copie et compléter l'arbre de probabilité
donné ci-dessous
{$E_{n+1}$}\rput(2.7,2.2){\dots}
\psline(2,1.5)(3.5,0.75)\rput[l](3.75,0.75){$\overline{E_{n+1}}$}\rput(2.7,0.7){\dots}
%
\psline(0,0)(1.5,-1.5)\rput(1.75,-1.5){$\overline{E_n}$}\rput(0.7,-1.2){\dots}
\psline(2,-1.5)(3.5,-0.75)\rput[l](3.75,-0.75){$E_{n+1}$}\rput(2.7,-0.7){\dots}
\psline(2,-1.5)(3.5,-2.25)\rput[l](3.75,-2.25){$\overline{E_{n+1}}$}\rput(2.7,-2.2){\dots}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapSuitesProba/ex113.Pspe/16.png)
- Montrer que, pour tout entier naturel
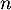 supérieur ou égal à
1,
supérieur ou égal à
1,
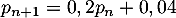 .
.
- Montrer que la suite
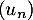 définie pour tout
entier naturel
définie pour tout
entier naturel 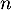 supérieur ou égal à 1 par
supérieur ou égal à 1 par
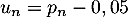 est une suite géométrique dont on donnera le premier terme
et la raison
est une suite géométrique dont on donnera le premier terme
et la raison 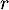 .
En déduire l'expression de
.
En déduire l'expression de 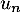 puis de
puis de 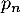 en fonction de
en fonction de
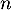 et
et 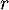 .
.
- En déduire la limite de la suite
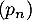 .
.
- On admet dans cette question que la suite
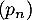 est croissante.
est croissante.
On considère le programme Python suivant :
![\[\fbox{
\begin{minipage}{8cm}
p=0\\
j=1\\
k=4\\
while (p $< 0.05 - 10**(-k))$:\\
\hspace*{1em}$p=0,2*p+ 0,04$\\
\hspace*{1em}$j=j+ 1$\\
print(j)
\end{minipage}}
\]](/Generateur-Devoirs/TS/ChapSuitesProba/ex113.Pspe/29.png)
À quoi correspond l'affichage final J ? Pourquoi est-on sûr que cet algorithme s'arrête ?
- Recopier sur la copie et compléter l'arbre de probabilité
donné ci-dessous
- Cette entreprise emploie 220 salariés. Pour la suite on admet
que la probabilité pour qu'un salarié soit malade une semaine donnée
durant cette période d'épidémie est égale à
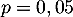 .
On suppose que l'état de santé d'un salarié ne dépend pas de l'état
de santé de ses collègues.
On désigne par
.
On suppose que l'état de santé d'un salarié ne dépend pas de l'état
de santé de ses collègues.
On désigne par 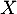 la variable aléatoire qui donne le nombre de
salariés malades une semaine donnée.
la variable aléatoire qui donne le nombre de
salariés malades une semaine donnée.
- Justifier que la variable aléatoire
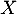 suit une loi binomiale
dont on donnera les paramètres.
Calculer l'espérance mathématique
suit une loi binomiale
dont on donnera les paramètres.
Calculer l'espérance mathématique 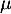 et l'écart type
et l'écart type 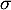 de la variable aléatoire
de la variable aléatoire 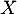 .
.
- Calculer la probabilité de l'événément: « le nombre de salariés absents dans l'entreprise au cours d'une semaine donnée est supérieur ou égal à 7 et inférieur ou égal à 15 ».
- Justifier que la variable aléatoire
Correction
Tags:ProbabilitésSuites
Voir aussi:
Quelques devoirs
Bac blanc: QCM: fonctions, convexité, suite et programme Python - Probabilités: test pour détecter une maladie - Suites: un peu sur les suites - Géométrie dans l'espace - Fonction logarithme
probabilités, loi binomiale et suites de probabilités - suites numériques
Fonction exponentielle - Géométrie dans l'espace - Probabilités, loi binomiale et arbre pondéré - Suite récurrente et python
Bac 2013, Amérique du Sud - Bac 2011, Amérique du nord
sur les probabilités: indépendance d'événements, arbre et probabilités conditionnelles, et le logarithme népérien (ln)
