Bac 2013 (Asie) - Un exercice bien complet sur les suites, et avec un algorithme
Exercice corrigé - Spécialité maths, terminale générale
Partie A
On considère la suite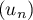 définie par:
définie par: 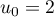 et, pour tout entier naturel
et, pour tout entier naturel 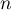 :
:
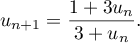
On admet que tous les termes de cette suite sont définis et strictement positifs.
Partie B
On considère la suite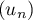 définie par:
définie par: 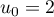 et, pour tout entier naturel
et, pour tout entier naturel 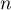 :
:
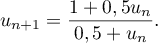
On admet que tous les termes de cette suite sont définis et strictement positifs.
Correction
On considère la suite
On admet que tous les termes de cette suite sont définis et strictement positifs.
- Démontrer par récurrence que, pour tout entier naturel
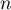 , on a :
, on a : 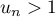 .
.
-
- Établir que, pour tout entier naturel
 , on a:
, on a: 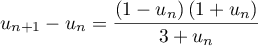 .
.
- Déterminer le sens de variation de la suite
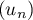 .
.
En déduire que la suite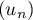 converge.
converge.
- Établir que, pour tout entier naturel
Partie B
On considère la suite
On admet que tous les termes de cette suite sont définis et strictement positifs.
- On considère l'algorithme suivant :

Reproduire et compléter le tableau suivant, en faisant fonctionner cet algorithme pour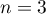 . Les valeurs de
. Les valeurs de 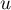 seront arrondies au millième.
seront arrondies au millième.
![\begin{tabular}{|*4{p{1.5cm}|}}\hline
\rule[1.3cm]{0.3cm}{-0.8cm}
$i$&1&2& 3\\ \hline
\rule[1.4cm]{0.3cm}{-0.8cm}
$u$&&&\\ \hline
\end{tabular}](/Generateur-Devoirs/TS/ChapSuites/ex113.Asie/18.png)
- Pour
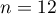 , on a prolongé le tableau précédent et on a obtenu :
, on a prolongé le tableau précédent et on a obtenu :
![\begin{tabular}{|c|*{9}{p{1.3cm}|}}\hline
\rule[1.3cm]{0.3cm}{-0.8cm}
$i$&4&5&6&7&8&9&10&11&12\\ \hline
\rule[1.3cm]{0.3cm}{-0.8cm}
$u$&\footnotesize{1,0083}&\footnotesize{0,9973}&\footnotesize{1,0009}&\footnotesize{0,9997}&\footnotesize{1,0001}&\footnotesize{0,99997}&\footnotesize{1,00001}&\footnotesize{0,999996}&\footnotesize{1,000001}\\ \hline
\end{tabular}](/Generateur-Devoirs/TS/ChapSuites/ex113.Asie/20.png)
Conjecturer le comportement de la suite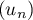 à l'infini.
à l'infini.
- On considère la suite
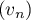 définie, pour tout entier naturel
définie, pour tout entier naturel 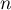 , par :
, par :  .
.
- Démontrer que la suite
 est géométrique de raison
est géométrique de raison  .
.
- Calculer
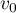 puis écrire
puis écrire 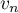 en fonction de
en fonction de 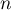 .
.
- Démontrer que la suite
-
- Montrer que, pour tout entier naturel
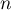 , on a:
, on a: 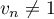 .
.
- montrer que, pour tout entier naturel
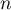 , on a:
, on a: 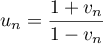 .
.
- Déterminer la limite de la suite
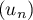 .
.
- Montrer que, pour tout entier naturel
Correction
Tag:Suites
Voir aussi:
Quelques devoirs
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
maison sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, suite auxiliaire arithmétique, convergence monotone et point fixe
