Suites: récurrences et limites
Corrigés des exercices
Calculs de limites
Démonstrations par récurrence
Rappel: principe de récurrence
Schéma général d'une démonstration par récurrence
On cherche à démontrer la propriété P(n)
Initialisation: Pour n = 0, on vérifie que la propriété P(0) est vraie.
Hérédité: Supposons que pour un certain entier n la propriété P(n) est vraie.
…
On montre alors, en utilisant la propriété P(n) (qui s'appelle alors l'hypothèse de récurrence) , que la propriété P(n+1) est encore vraie.
Conclusion: On vient de montrer, d'après le principe de récurrence, que la propriété P(n) est vraie pour tout entier n.
Exercice 2
Soit (un)
la suite définie par
u0 = 2
et, pour tout entier n,
un+1 = 5un + 4.
Montrer que, pour tout entier n, un > 0.
Exercice 3
Soit (un)
la suite définie par
u0 = −3
et, pour tout entier n,
un+1 = 5 − 4un.
Montrer que, pour tout entier n, un = (−4)n+1 + 1.
Exercice 4
Soit (un)
la suite définie par
u0 = 12
et, pour tout entier n,
un+1 = un + 1un + 2.
Montrer que, pour tout entier n, 0 < un < 1.
Exercice 5
On note, pour tout entier k non nul,
k! = k×(k−1)×(k−2)×…×2×1 .
Montrer que, pour tout entier n ≥ 1,
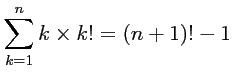 .
.
Exercice 6
Soit (un)
la suite définie par
u0 = 1,
u1 = 2,
et, pour tout entier n,
par la relation
un+2 = 5un+1 − 6un.
- Calculer
u2,
u3
et
u4.
- Démontrer que, pour tout entier n, on a un = 2n.
Voir aussi: