Suites: études, récurrences, convergences
Exercices complets corrigés
Calculs de limites
Démonstrations par récurrence
Convergence monotone et point fixe
Théorèmes de comparaison, théorème des gendarmes
Exercices complets avec suite auxiliaire et sommes et produit des termes
Exercice 15
On considère la suite - Calculer
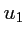 et
et 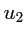 .
.
- Démontrer que, pour tout entier
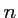 ,
,
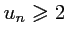 .
.
- Montrer que
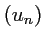 est une suite décroissante.
est une suite décroissante.
- Montrer que la suite
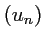 est convergente et déterminer sa limite.
est convergente et déterminer sa limite.
- On pose, pour tout entier
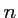 ,
, 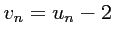 .
.
Montrer que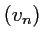 est une suite géométrique.
est une suite géométrique.
En déduire l'expression de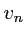 en fonction de
en fonction de 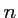 .
.
- Soit
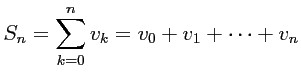 et
et
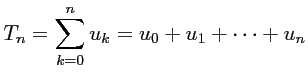 .
.
Déterminer l'expression de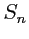 , puis de
, puis de 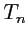 , en fonction de
, en fonction de
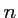 .
.
- Déterminer
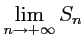 et
et
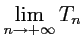 .
.
Exercice 16
Soit la suite numérique (un)
définie sur
N*
par
un
= n(n + 2)
(n + 1)2
.
-
- Montrer que, pour tout n∈N*,
un
= 1 − 1
(n + 1)2
.
- Prouver que, pour tout n∈N*,
0 < un < 1.
- Étudier le sens de variation de la suite (un) .
- Montrer que, pour tout n∈N*,
un
= 1 − 1
(n + 1)2
.
- On pose xn = u1 × u2 × … × un .
- Démontrer par récurrence que, pour tout entier n non nul, on a
xn
= n + 2
2(n + 1)
- Déterminer la limite de la suite (xn) .
- Démontrer par récurrence que, pour tout entier n non nul, on a
xn
= n + 2
2(n + 1)
Voir aussi: