Réviser, approfondir son année de terminale

et préparer son entrée en prépa (et/ou ailleurs aussi)
Télécharger le sujet pdf

Fonctions


Pour quelques révisions plus basiques, voir éventuellement ces quelques fonctions à étudier.
Exercice 19
Soit $\lambda$ un nombre réel strictement positif et $f_\lambda$ la fonction définie sur $\R_+^*$ par
\[f_\lambda(x)=\dfrac{\lambda x^2}2-\ln(x)\]

Déterminer le minimum de cette fonction.


Exercice 20: Fonctions hyperboliques
Les fonctions $ch$ (cosinus hyperbolique) et $sh$ (sinus hyperbolique) sont définies par
\[ch(x)=\dfrac{e^x+e^{x}}2\]
et
\[sh(x)=\dfrac{e^x-e^{-x}}2\]
  1. Étudier ces deux fonctions, variations et limites, et tracer leur courbe.
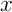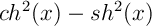
  2. Calculer, pour $x$ réel,   $ch^2(x)-sh^2(x)$

Remarque: Ces fonctions sont nommées ainsi par analogie avec les fonctions trigonométriques et leurs expressions complexes (formule d'Euler):
\[\cos(x)=\dfrac{e^{ix}+e^{-ix}}2\]

et
\[\sin(x)=\dfrac{e^{ix}-e^{-ix}}{2i}\]

pour lesquelles on calcule aussi (à faire avec les formules précédentes !) l'identité analogue
\[\cos^2(x)+\sin^2(x)=1\]

Exercice 21
Soit $g$ la fonction définie sur $]0;+\infty[$ par $g(x)=x^2+\ln(x)$.
  1. Dresser le tableau de variation de 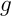$g$. Préciser les limites.
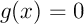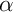  2. Montrer que l'équation $g(x)=0$ admet une unique solution $\alpha$.
    Donner un encadrement de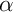 $\alpha$ d'amplitude $10^{-2}$.
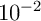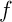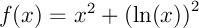  3. Soit $f$ la fonction définie $]0;+\infty[$ par $f(x)=x^2+\lp\ln(x)\rp^2$.
    Montrer que $f$ admet un minimum en $x=\alpha$.

Voir aussi:
LongPage: h2: 1 - h3: 0