Réviser, approfondir son année de terminale

et préparer son entrée en prépa (et/ou ailleurs aussi)
Télécharger le sujet pdf

Calcul de dérivées et tangentes

Exercice 16
Calculer les fonctions dérivées des fonctions suivantes (sans se préoccuper des ensembles de définition):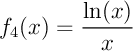
$f_1(x)=3x^7-2x^4+\dfrac32x^2-\sqrt5$      $f_2(x)=\dfrac{2x-1}{5-3x}$      $f_3(x)=x\ln(x)$      $f_4(x)=\dfrac{\ln(x)}x$ $f_5(x)=2x^2e^x$      $f_6(x)=e^{x^2-3x+1}$      $f_7(x)=e^{\frac1{\sqrt{x}}}$      $f_8(x)=\dfrac{1-e^{-x}}x$      $f_9(x)=ln\lp e^{2x+1}+1\rp$      $f_{10}(x)=e^{\sqrt{3x^2+2}}$      $f_{11}(x)=\ln(\cos(2x))$      $f_{12}(x)=\ln(\ln(x))$      $f_{13}(x)=\ln(\ln(\ln(x)))$      $f_{14}(x)=x^4\cos\lp 2x+1\rp$      $f_{15}(x)=\sqrt{\ln(2x+3)}$


Exercice 17
Soit $k$ un réel non nul et $f$ la fonction $f:x\mapsto kx^2$.
On note $A$, $B$ et $I$ les points de la courbe de $f$ d'abscisses respectives $a$, $b$ et   $\dfrac{a+b}2$.
Montrer que la droite $(AB)$ est parallèle à la tangente à la courbe de $f$ en $I$.

Exercice 18
Une fonction $f$ dérivable sur un intervalle $I$ est convexe lorsque sa courbe représentative est au dessus de toutes ses tangentes.
  1. Montrer que la fonction carré est convexe.
  2. Montrer que la fonction exponentielle est convexe.

Voir aussi, exercices corrigés:
LongPage: h2: 1 - h3: 0