Réviser, approfondir son année de terminale

et préparer son entrée en prépa (et/ou ailleurs aussi)
Télécharger le sujet pdf

Exponentielle, ln, suite, intégrales, ... de tout à la fois


Exercice 22
Soit 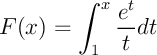$F$ la fonction définie sur $]0;+\infty[$ par $\dsp F(x)=\int_1^x\dfrac{e^t}{t}dt$.
  1. Déterminer le sens de variation de $F$.
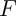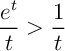  2. Prouver que, pour tout $t>0$, $\dfrac{e^t}{t}>\dfrac1t$.
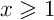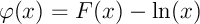    En déduire, pour $x\geqslant 1$, le signe de $\varphi(x)=F(x)-\ln(x)$.
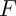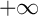  3. Déduire de cette étude le comportement de $F$ en $+\infty$.

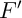  1. Que vaut $F'$ ? quel est son signe ?
  2. La fonction exponentielle est strictement croissante donc pour $t>0$ ..., puis en divisant par $t>0$ ...
    En intégrant l'inégalité précédente ...
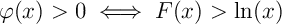  3. $\varphi(x)>0\iff F(x)>\ln(x)$ puis par le (corollaire du) théorème des gendarmes,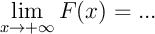 $\dsp\lim_{x\to+\infty}F(x)=...$



Exercice 23
On s'intéresse à la valeur de la limite de la somme
\[\bgar{ll}S_n&=\dsp\sum_{k=0}^n\dfrac{(-1)^k}{k+1}\\ &=1-\dfrac12+\dfrac13-\dfrac14+ \dots + \dfrac{(-1)^n}{n+1}\enar\]

L'objectif est de montrer que cette somme converge, lorsque $n\to+\infty$, et de déterminer cette limite.
Remarque: cette limite se note alors
\[\sum_{k=0}^{+\infty}\dfrac{(-1)^k}{k+1}\]

et s'appelle une série. Il s'agit ici en plus d'une série courante: la série harmonique alternée
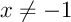  1. Soit $x\not=-1$, montrer que
    \[\sum_{k=0}^n(-1)^kx^k=\dfrac1{1+x}+\dfrac{(-1)^nx^{n+1}}{1+x}\]

  2. En déduire que
    \[\sum_{k=0}^n\dfrac{(-1)^k}{1+k}=\ln(2)+(-1)^n\int_0^1\dfrac{x^{n+1}}{1+x}dx\]

  3. Montrer que
    \[0\leqslant\int_0^1\dfrac{x^{n+1}}{1+x}dx\leqslant\dfrac1{n+2}\]

  4. Conclure que
    \[\lim_{n\to+\infty}\sum_{k=0}^n\dfrac{(-1)^k}{1+k}=\ln(2)\]


  1. Il s'agit de la somme des termes consécutifs d'une suite géométrique de raison $-x$.
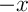  2. On intègre terme à terme, grâce à la linéarité de l'intégrale, l'égalité précédente entre 0 et 1.
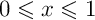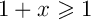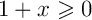  3. On encadre, pour $0\leqslant x\leqslant1$, on a $1+x\geqslant1$ et $1+x\geqslant0$ d'où
    \[0\leqslant\dfrac1{1+x}\leqslant1\]

    puis, en multipliant par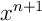 $x^{n+1}$ et enfin comme l'intégrale conserve l'ordre, on intègre chaque terme de cette dernière inégalité.
  4. On utilise alors le théorème des gendarmes pour l'inégalité précédente et l'égalité de la question 2.


Exercice 24
Pour tout entier naturel $n$ non nul, on associe la fonction $f_n$ définie sur $\R$ par:
\[f_n(x)=\dfrac{4e^{nx}}{e^{nx}+7}\]


On désigne par $\mathcal{C}_n$ la courbe représentative de la fonction $f_n$ dans un repère orthonormal.
  1. Étude de la fonction $f_1$
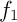
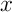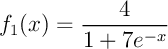    1. Vérifier que, pour tout réel $x$, $f_1(x)=\dfrac4{1+7e^{-x}}$.
    2. Démontrer que la courbe 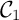$\mathcal{C}_1$ admet deux asymptotes dont on précisera les équations.
    3. Démontrer que la fonction 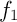$f_1$ est strictement croissante sur $\R$.
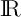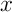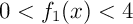    4. Démontrer que, pour tout réel $x$, on a $0<f_1(x)<4$.
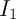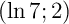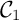    5. Démontrer que le point $I_1$ de coordonnées $\lp\ln7;2\rp$ est un centre de symétrie de la courbe $\mathcal{C}_1$.
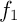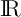    6. Déterminer une primitive de la fonction $f_1$ sur $\R$ et en déduire la valeur moyenne de 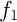$f_1$ sur l'intervalle $[0;\ln7]$.

  2. Étude de certaines propriétés de la fonction $f_n$.
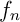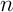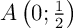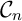    1. Démontrer que pour tout entier $n$ non nul, le point $A\lp0;\frac12\rp$ appartient à la courbe $\mathcal{C}_n$.
    2. Démontrer que, pour tout entier 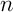$n$ non nul, la courbe 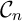$\mathcal{C}_n$ et la droite d'équation 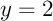$y=2$ ont un unique point d'intersection 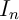$I_n$ dont on précisera l'abscisse.
    3. Déterminer une équation de la tangente 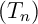$(T_n)$ à la courbe 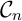$\mathcal{C}_n$ au point $I_n$.
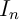    4. Soit la suite 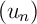$\lp u_n\rp$ définie, pour tout entier naturel 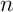$n$, par:
      \[u_n=\dfrac{n}{\ln7}\int_0^{\frac{\ln7}n}f_n(x)dx\]
      Montrer que cette suite est constante.

Voir aussi:
LongPage: h2: 1 - h3: 0