Réviser, approfondir son année de terminale
et préparer son entrée en prépa (et/ou ailleurs aussi)
Nombres complexes
Pour reprendre à la base, voir là par exemple.
Exercice 10
Écrire sous forme algébrique: 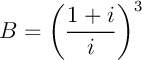
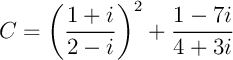
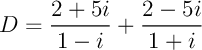
Exercice 11
Écrire sous forme exponentielle: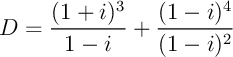
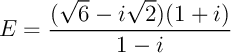
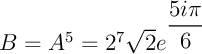
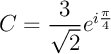
Exercice 12
On considère le nombre complexe - Ecrire
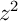 sous forme algébrique.
sous forme algébrique.
- Déterminer le module et la mesure principale de l'argument de
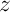 .
.
-
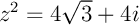
- On a donc,
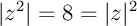 donc
donc 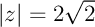 .
.
Pour l'argument,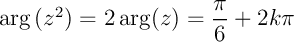 ,
, 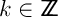 .
donc
.
donc 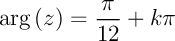 ,
d'où
,
d'où 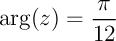 ou
ou
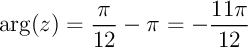 .
.
Comme la partie réelle de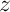 est positive
est positive 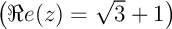 ,
on a nécessairement
,
on a nécessairement 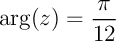 .
.
Exercice 13
Pour quels entiers naturels
On passe par la forme exponentielle, et on obtient
qu'il s'agit d'un nombre réel si et seulement si 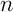 est un multiple de 6.
est un multiple de 6.
Exercice 14
Montrer que, pour tous nombres complexes
La définition 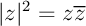 , donc aussi
, donc aussi
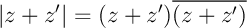 et
et 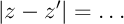 ,
permet de développer et de mener les calculs...
,
permet de développer et de mener les calculs...
On peut aussi revenir à la forme algébrique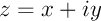 et
et 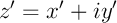 et calculer séparemment les deux côtés de l'égalité pour s'apercevoir qu'ils sont bien égaux.
et calculer séparemment les deux côtés de l'égalité pour s'apercevoir qu'ils sont bien égaux.
On peut aussi revenir à la forme algébrique
Exercice 15
Déterminer l'ensemble des nombres complexes
Méthode algébrique: on aboutit à 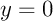 qui est l'équation (de droite) de l'axe des abscisses
qui est l'équation (de droite) de l'axe des abscisses
Méthode géométrique: on pose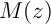 ,
, 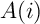 et
et 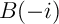 , alors l'équation se réécrit géométriquement
, alors l'équation se réécrit géométriquement 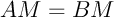 et l'ensemble des points
et l'ensemble des points 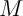 recherchés est excatement la médiatrice de
recherchés est excatement la médiatrice de ![$[AB]$](doc-II-complexes-light-IMG/55.png) qui est l'axe des abscisses.
qui est l'axe des abscisses.
Méthode géométrique: on pose
Voir aussi: