Nombres complexes


Forme trigonométrique d'un nombre complexe


Définition: Coordonnées polaires
Dans le plan un point M peut-être repéré par ses coordonnées cartésienne (x ; y), ou son affixe complexe z = x + iy.
Il existe d'autres méthodes pour repérer un point dans le plan. On peut aussi définir un point en donnant sa distance à l'origine et un angle, par exemple l'angle par rapport à l'axe des abscisses.
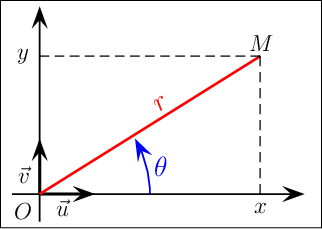
Illustration: coordonnées polaires et sartésiennes

On appelle coordonnées polaires le couple (r ; θ) avec r = OM et l'angle θ = ( u ; OM ).


Si z = x + iy est l'affixe du point M, alors les coordonnées (r ; θ) sont le couple module et argument du nombre complexe z.
On a donc
r = z = x2 + y2
et la trigonométrie des triangles rectangles donne
cos(θ) = x/r
et
sin(θ) = y/r
ou aussi, en inversant ces deux dernières relations
x = r cos(θ) y = r sin(θ)
On peut alors reporter ces expressions dans l'expression algébrique z = x + iy:

Définition
L'affixe z du point M s'écrit alors,
z = r (cos(θ) + i sin(θ))
Cette écriture est la forme trigonométrique de z et met en évidence les coordonnées polaires (r ; θ) du point M d'affixe z.


Méthode pour écrire un nombre complexe sous forme trigonométrique
Pour un nombre complexe z = x + iy, on calcule tout d'abord son module puis on écrit le cosinus et le sinus de l'argument à partir desquels on détermine l'argument.
Connaissant finalement r et θ, il n'y a plus qu'à écrire la forme trigonométrique précédente.

Exemple/exercice
Écrire sous forme trigonométrique z = 1 + i.
On calcule le module 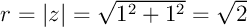$r=|z|=\sqrt{1^2+1^2}=\sqrt2$, puis l'argument 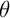$\theta$ est tel que
\[\la\bgar{ll}\cos\theta=\dfrac{x}{r}=\dfrac1{\sqrt2}=\dfrac{\sqrt2}2\\ \sin\theta=\dfrac{y}{r}=\dfrac1{\sqrt2}=\dfrac{\sqrt2}2\enar\right.\]

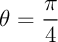L'angle correspondant est $\theta=\dfrac\pi4$, et alors l'écriture trigonométrique est
\[\bgar{ll}&z=1+i\\&=\sqrt2\lp\cos\dfrac\pi4+i\sin\dfrac\pi4\rp\enar\]


Les coordonnées polaires peuvent se trouver aussi directement graphiquemet:
pspicture\rput[r](1,1.2){$M$}\psarc{->}(0,0){2}{0}{45}$\theta=\dfrac\pi4$


Écrire sous forme trigonométrique z = 1 − i3.
On calcule le module 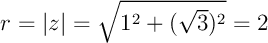$r=|z|=\sqrt{1^2+(\sqrt3)^2}=2$, puis l'argument 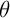$\theta$ est tel que
\[\la\bgar{ll}\cos\theta=\dfrac{x}{r}=\dfrac12\\ \sin\theta=\dfrac{y}r=-\dfrac{\sqrt3}2\enar\right.\]

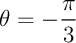L'angle correspondant est $\theta=-\dfrac\pi3$, et alors l'écriture trigonométrique est
\[\bgar{ll}&z=1+i\\&=2\Biggl(\cos\lp-\dfrac\pi6\rp+i\sin\lp-\dfrac\pi6\rp\Biggr)\enar\]



Exercice 17
Écrire sous forme trigonométrique les nombres complexes suivants:
  1. z1 = 3
    On peut appliquer la méthode générale précédente:
    z1 = 3 = 3
    et l'argument θ est tel que
    cos(θ) = x/r = 3/3 = 1 sin(θ) = x/r = 0/3 = 0
    d'où θ = 0 et l'écriture trigonométrique
    z1 = 3 (cos(0) + i sin(0))

    Géométriquement, ce cas est simple: le point M d'affixe complexe z1 = 3 est sur l'axe des abscisses (axe réel)
    M sur l'axe réel
  2. z2 = −4
    On peut utiliser la méthode calculatoire générale:
    z2 = −4 = 4
    et l'argument θ est tel que
    cos(θ) = x/r = −4/4 = −1 sin(θ) = x/r = 0/4 = 0
    d'où θ = π et l'écriture trigonométrique
    z2 = 4 (cos(π) + i sin(π))

    Géométriquement, ce cas est simple aussi: le point M d'affixe complexe z2 = −4 est sur l'axe des abscisses (axe réel)
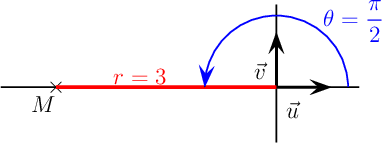
    M sur l'axe réel
  3. z3 = 2i
    On peut utiliser la méthode calculatoire générale:
    z3 = 2i = 2
    et l'argument θ est tel que
    cos(θ) = x/r = 0/2 = 0 sin(θ) = x/r = 2/2 = 1
    d'où θ = π/2 et l'écriture trigonométrique
    z1 = 2 cos(π/2) + i sin(π/2)

    Géométriquement, ce cas est simple aussi: le point M d'affixe complexe z3 = 2i est sur l'axe des ordonnées (axe imaginaire pur)
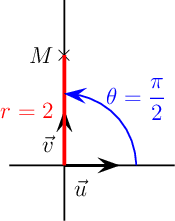
    M sur l&axe; imaginaire
  4. z4 = −1 + i
    On peut utiliser la méthode calculatoire générale:
    z4 = −1 + i = (−1)2 + 12 = 2
    et l'argument θ est tel que
    cos(θ) = −1/2 = −2/2 sin(θ) = 1/2 = 2/2
    d'où θ = 3π/4 et l'écriture trigonométrique
    z1 = 2 cos(3π/4) + i sin(3π/4)

    Géométriquement, on peut aussi trouver les coordonnées polaires:
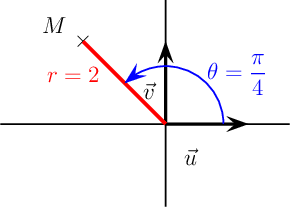
    Coordonnees polaires de M
  5. z5 = −3 + i
    Comme d'habitude maintenant,
    z5 = −3 + i = (−3)2 + 12 = 4 = 2
    et l'argument θ est tel que
    cos(θ) = −3/2 sin(θ) = 1/2
    d'où θ = 5π/6 et l'écriture trigonométrique
    z5 = 2 cos(5π/6) + i sin(5π/6)
  6. z6 = −63 + 6i
    Comme d'habitude maintenant,
    z6 = −63 + 6i = (−63)2 + 62 = 144 = 12
    et l'argument θ est tel que
    cos(θ) = −63/12 = −3/2 sin(θ) = 6/12 = 1/2
    d'où θ = 5π/6 et l'écriture trigonométrique
    z1 = 12 cos(5π/6) + i sin(5π/6)


    Remarque: on a z7 = 6z6, calculé à la question précédente, d'où le résultat en multipliant aussi par l'expression trouvée pour la forme trigonométrique de z6.
  7. z7 = 6 + i2
    Comme d'habitude,
    z6 = 6 + i2 = 62 + 22 = 8 = 22
    et l'argument θ est tel que
    cos(θ) = 6/22 = 3/2 sin(θ) = 2/22 = 1/2
    d'où θ = π/6 et l'écriture trigonométrique
    z1 = 22 cos(π/6) + i sin(π/6)


LongPage: h2: 2 - h3: 0