Nombres complexes


Module et argument d'un nombre complexe


Définition
On appelle module du nombre complexe z = x + iy, avec x∈R et y∈R, le nombre
z = x2 + x2
Géométriquement, si M est le point d'affixe z dans le plan complexe, alors le module de z est la distance OM.

L'argument du nombre complexe non nul z est une mesure de l'angle orienté:
arg(z) = ( u ; OM )
Représentation graphique du module et argument d'un nombre complexe


Remarques:
  • Un nombre complexe non nul z a une infinité d'arguments: si θ est un de ses arguments, alors tous les autres sont de la forme θ + 2kπ, pour tout eniter relatif k.
    On note néanmoins souvent, plus simplement mais par abus de notation, arg(z) = θ.
  • Si z est un réel (z = x + 0i), alors z = x: le module coïncide avec la valeur absolue pour les nombres réels (d'où la notation d'ailleurs).
    Par exemple, 6 = 6 et −3 = 3.



Exercice 13
Calculer les modules des nombres complexes suivants:
  1. z1 = 1 + 2i
    z1 = 12 + 22 = 5
  2. z2 = 2 − 3i
    z2 = 22 + (−3)2 = 13
  3. z3 = −1 − 5i
    z3 = (−1)2 + (−5)2 = 26
  4. z4 = 3
    z4 = 32 = 3
    Remarque: pour un nombre réel, le module coïncide avec la valeur absolue, d'où la notation.
  5. z5 = −6
    z5 = (−6)2 = 6
    Remarque: pour un nombre réel, le module coïncide avec la valeur absolue, d'où la notation.
  6. z6 = 8i
    z6 = 82 = 8
  7. z7 = −3i
    z7 = (−3)2 = 3
  8. z8 = 3 + i
    z8 = 32 + 12 = 4 = 2



Propriété
Soit A(zA) et B(zB), alors AB(zB − zA) et
  • AB = zB − zA
  • ( u, AB ) = arg(zAB) = arg(zB − zA) .
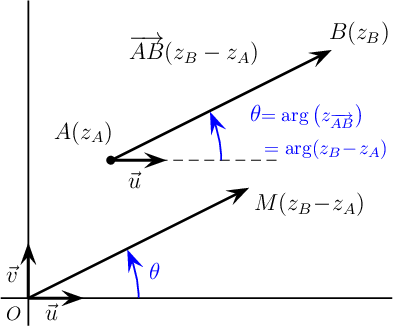
Angle et module pour deux points



Exercice 14
Déterminer l'ensemble des nombres complexes z, et représenter graphiquement ces solutions, tels que:
  1. arg(z) = π/6
    En appliquant directement la définition, il s'agit géométriquement d'une demi-droite: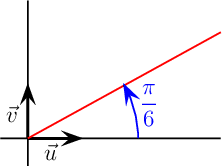
    Demi-droite des points d'argument pi/6
  2. z − 3 = z + 2i
    Il faut connaître les deux méthodes, géométrique et algébrique.

    Méthode géométrique
    Soit M d'affixe z un des points recherchés. En notant A le point d'affixe zA = 3 et B le point d'affixe zB = −2i et on a alors, en interprétant les modules par des longueurs:
    z − 3 = z + 2i ⇔ AM = BM
    Ainsi, M est équidistant des points A et B: l'ensemble des points recherchés est la médiatrice de [AB].
    Médiatrice de [AB]



    Méthode algébrique
    On pose z = x + iy et alors
    z − 3 = x − 3 + iy
    d'où
    z − 3 = (x − 3)2 + y2
    et de même
    z + 2i = x + i(y + 2)
    d'où
    z + 2i = x2 + (y + 2)2
    On a alors, en élevant au carré ces nombres positifs, puis en développant
    z − 3 = z + 2i ⇔ z − 32 = z + 2i2 ⇔ (x − 3)2 + y2 = x2 + (y + 2)2
    puis, en développant les identités remarquables, les carrés se simplifient, et en isolant finalement y on obtient l'équation réduite de droite:
    y = −6/4x + 5/4
    qui est l'équation de la médiatrice de [AB] trouvée par la méthode géométrique.
  3. z + 1 − 2i < 5
    Géométriquement, on pose M le point d'affixe z et A le point d'affixe
    zA = −(1 − 2i) = −1 + 2i
    de telle façon que l'inéquation proposée s'écrive
    z + 1 − 2i<5 ⇔ AM<5
    Les solutions sont donc tous les points dont la distance à A est strictement plus petite que 5: c'est le disque ouvert de rayon 5 et de centre A.
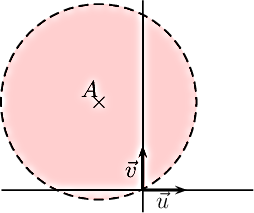
    Disque solution
  4. arg(z + i) = π
    D'après la propriété précédente, en posant A le point d'affixe zA = −i et M le point recherché d'affixe z , on a
    arg(z + i) = π ⇔ ( u ; AM ) = π
    et les solutions sont donc les points de la demi-droite suivante: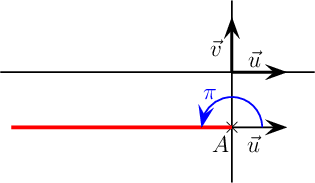
    Demi-droite solution



Exercice 15
Dans le plan complexe, A, B et C sont les points d'affixes: zA = 1 + i, zB = 4 + 5i et zC = 5 − 2i.
  1. Montrer que AB = AC.
    1. Déterminer l'affixe du point G tel que le quadrilatère AGBC soit un parallélogramme.
    2. Déterminer les affixes des points I et J, milieux respectifs de [GC] et [AB].



Propriétés algébriques du module
Pour tous nombres complexes z et z':
  • zz = z2 = x2 + y2, pour z = x + iy avec x∈R et y∈R.
  • −z = z
  • z = z
  • z + z' ≤ z + z' (inégalité triangulaire)
  • z z' = zz'
    et donc zn = zn
  • z/z' = z/z'



Exercice 16
Calculer le module des nombres complexes suivants:
  1. z = 1 + i/3 − 4i
    En utilisant la règle précédente sur le module d'un quotient:
    z = 1 + i/3 − 4i = 1 + i/3 − 4i = 12 + 12/32 + (−4)2 = 2/5
  2. z = (2 + 2i)(−1 + i)
    En utilisant la règle précédente sur le module d'un produit:
    z = 2 + 2i−1 + i = 22 + 22(−1)2 + 12 = 82 = 16 = 4
  3. z = i(−1 − i)/−3 + 4i
    En utilisant les règles sur le module d'un quotient et d'un produit:
    z = i(−1 − i)/−3 + 4i = i−1 −i/−3 + 4i = 1×(−1)2 + (−1)2/(−3)2 + 42 = 2/5
  4. z = −4(2 −i)/2i(1 + 2i)
    De même que pour le calcul précédent,
    z = −4(2 −i)/2i(1 + 2i) = −42 −i/2i1 + 2i = 4×22 + (−1)2/212 + 22 = 45/25 = 2


LongPage: h2: 2 - h3: 0