Trois petites équations, fractions et quotients...
Exercice corrigé - maths en seconde générale
Énoncé
Résoudre les équations:
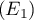 :
: 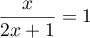
 :
: 
 :
: 
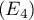 :
: 
Correction
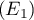 :
:
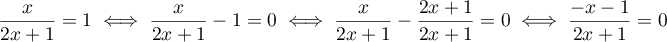
C'est une équation quotient, et donc,
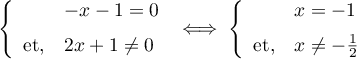 ,
d'où
,
d'où 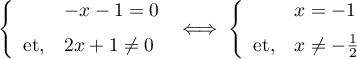 .
.
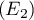 :
:
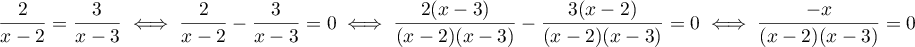 .
.
C'est une équation quotient, et donc,
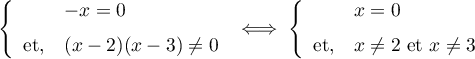 ,
d'où,
,
d'où,
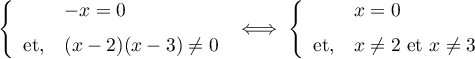 .
.
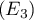 :
:
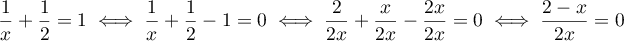 .
.
C'est une équation quotient et donc,
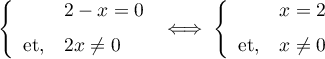 ,
d'où,
,
d'où,
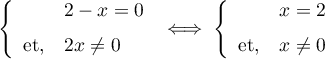 .
.
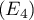 :
:
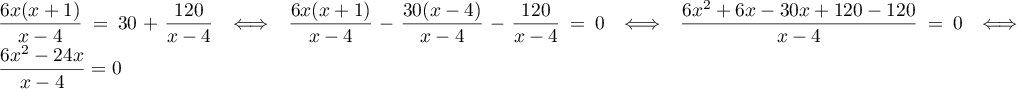
On peut, et doit, factoriser le numérateur: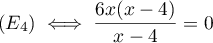
C'est une équation quotient, et donc,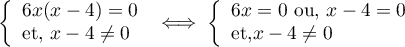
Finalement, cette équation a une seule solution: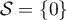 .
.
Correction
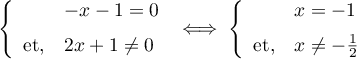 ,
d'où
,
d'où 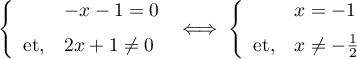 .
.
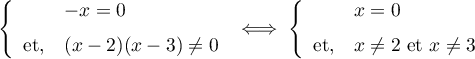 ,
d'où,
,
d'où,
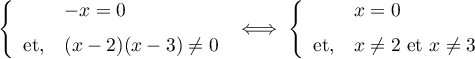 .
.
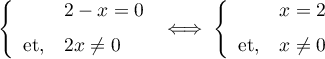 ,
d'où,
,
d'où,
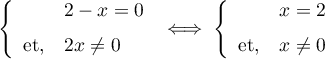 .
.
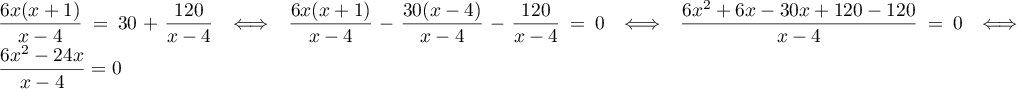
On peut, et doit, factoriser le numérateur:
C'est une équation quotient, et donc,
Finalement, cette équation a une seule solution:
Tag:Équations
Voir aussi:
Quelques devoirs
calcul algébrique: calculs avec des puissance, factoriser des expressions algébriques, et résoudre des premières équations
sur la résolution d'équations (produit nul, quotient nul, équation avec un carré) et deux fractions avec des puissances à simplifier
sur quelques équations à résoudre, systèmes d'équations à deux inconnues, et la construction géométrique graphique de points et vecteurs
sur les vecteurs et coordonnées: calculs de coordonnées, et montrer l'alignement de points. Quelques équations et un système à résoudre
sur les équations, inéquations et tableaux de signes
