Production d'objets pouvant posséder 2 défauts
Exercice corrigé - maths en seconde générale
Énoncé
Une usine fabrique des articles en grande quantité, dont certains sont
défectueux à cause de deux défauts possibles, un défaut d'assemblage
ou un défaut de dimension.
Une étude statistique a permis de constater que 12% des articles fabriqués sont défectueux: 8% des articles fabriqués ont un défaut d'assemblage et 6% des articles fabriqués ont un défaut de dimension.
On choisit au hasard un article et on note :
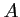 l'évènement : «Un article prélevé au hasard présente un
défaut d'assemblage »
l'évènement : «Un article prélevé au hasard présente un
défaut d'assemblage »
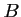 l'évènement : «Un article prélevé au hasard présente un
défaut de dimension »
l'évènement : «Un article prélevé au hasard présente un
défaut de dimension »
-
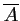 et
et
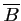 les évènements contraires
respectifs de
les évènements contraires
respectifs de 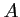 et
et 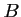 .
.
- Grâce aux données de l'énoncé :
- a. Donner les probabilités
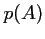 et
et 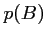 ;
;
- b. Traduire par une phrase l'évènement
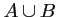 . Donner la
probabilité de l'évènement
. Donner la
probabilité de l'évènement 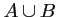 .
.
- a. Donner les probabilités
- Quelle est la probabilité de l'évènement «un article prélevé
au hasard ne présente aucun défaut »?
- Exprimer en utilisant les événements
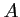 et
et 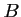 l'événement
«un article prélevé au hasard présente les deux défauts »,
puis calculer sa probabilité.
l'événement
«un article prélevé au hasard présente les deux défauts »,
puis calculer sa probabilité.
Correction
Correction
- a)
- D'après l'énoncé,
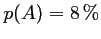 et
et
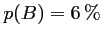 .
.
- b)
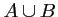 est l'événement:
«l'article prélevé au hasard présente soit un défaut d'assemblage,
soit un défaut de dimensionnement», c'est-à-dire,
est l'événement:
«l'article prélevé au hasard présente soit un défaut d'assemblage,
soit un défaut de dimensionnement», c'est-à-dire,
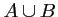 est l'événement: «l'article est défectueux».
est l'événement: «l'article est défectueux».
La probabilité de l'évènement
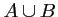 est donc
est donc
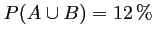 .
.
- L'évènement «un article prélevé au hasard ne présente aucun
défaut »est l'événement contraire de
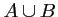 .
Ainsi, sa probabilité est de
.
Ainsi, sa probabilité est de
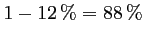 ".
".
- «un article prélevé au hasard présente les deux défauts »
est l'événement
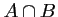 ; il a pour probabilité:
; il a pour probabilité:
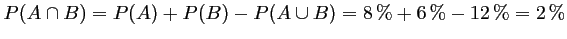 .
.
Tag:Probabilités
Voir aussi:
Quelques devoirs
pourcentage et probabilités, et deux tableaux de signes. Intersection de deux courbes
probabilités (arbres de probabilités), et quelques inéquations (tableaux de signes)
tableau de signe - Intersection et position relative de deux courbes - Taux d'évolution successifs - Système d'équations - Équations cartésienne de droites et intersection de droites - Probabilité: un jeu avec un dé - Probabilité: patisserie à la crème ou aux fruits
tableau de signe - Intersection et position relative de deux courbes - Taux d'évolution successifs - Système d'équations - Équations cartésienne de droites et intersection de droites - Probabilité: un jeu avec un dé - Probabilité: véhicules avec d'éventuels problèmes de frein et/ou d'éclairage
tableau de signe - Équations cartésienne de droites - Système d'équations - Équations cartésienne de droites et intersection de droites - Probabilité: au hasard, une pièce truquée ou une équlibrée
