Un système d'équations trigonométriques

Colle de mathématiques

Sujet de colle de maths:

ComplexesNombres complexs

Énoncé du sujet

Soit 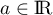$a\in\R$ . Résoudre le système $\la\begin{array}{ll} \cos a +\cos(a+x)+\cos(a+y)=0 \\[.3em] \sin a +\sin(a+x)+\sin(a+y)=0 \enar\right.$

Correction

Le système est équivalent à

$\begin{array}{ll} e^{ia}+e^{i(a+x)}+e^{i(a+y)}=0 &\iff e^{ia}\left( 1+e^{ix}+e^{iy}\rp=0 \\ &\iff 1+e^{ix}+e^{iy}=0 \\ &\iff e^{i\frac{x+y}{2}}\left( e^{i\frac{x-y}{2}}+e^{-i\frac{x-y}{2}}\rp=-1 \\ &\iff 2e^{i\frac{x+y}{2}}\cos\lp\dfrac{x-y}{2}\rp=-1 \\ &\iff \la\begin{array}{ll} 2\cos\lp\dfrac{x+y}{2}\rp\cos\lp\dfrac{x-y}{2}\rp=-1\\ 2\sin\lp\dfrac{x+y}{2}\rp\cos\lp\dfrac{x-y}{2}\rp=0\\ \enar\right.\\[2em] &\iff \la\begin{array}{ll} \cos x+\cos y=-1\\ \sin x+\sin y=0\\ \enar\right.\\[1em] \end{array}$

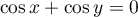On a ainsi $\sin x=-\sin y=\sin(-y)\iff x\equiv-y\,[2\pi]$ et alors $\cos x+\cos y=2\cos y=-1\iff y\equiv\dfrac{2\pi}{3}\,[2\pi]$ ou $y\equiv -\dfrac{2\pi}{3}\,[2\pi]$ , ou, $x\equiv\pi+y\,[2\pi]$ et alors $\cos x+\cos y=0$ ce qui est impossible.

Tag:Complexes

Autres sujets au hasard: