Trouver les parametres d'une loi normale
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires continuesVariables aléatoires continues
Énoncé du sujet
Soit 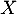 une variable aléatoire qui suit la loi normale
une variable aléatoire qui suit la loi normale 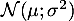 .
On sait de lus que
.
On sait de lus que 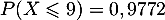 et
et  .
Calculer
.
Calculer 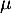 et
et 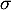 .
.
On donne les valeurs de la fonction de répartition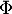 de la loi normale centrée réduite:
de la loi normale centrée réduite:
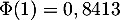 ,
, 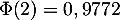 ,
,  .
.
On donne les valeurs de la fonction de répartition
Correction
 et
et 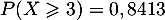 .
.
On se ramène à une loi normale centrée réduite, en posant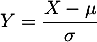 et alors,
et alors,
![\[P(X\leqslant9)=P\left( Y\leqslant\dfrac{9-\mu}\sigma\rp=0,9772\]](/Generateur-Devoirs/Colles/VAC/determiner-loi-normale_c/4.png)
soit donc
![\[\Phi\lp\dfrac{9-\mu}\sigma\rp=0,9772=\Phi(2)\]](/Generateur-Devoirs/Colles/VAC/determiner-loi-normale_c/5.png)
Comme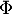 est bijective, on en déduit que
est bijective, on en déduit que
![\[\dfrac{9-\mu}\sigma=2\]](/Generateur-Devoirs/Colles/VAC/determiner-loi-normale_c/7.png)
De même,
![\[\begin{array}{ll}P(X\geqslant3)&=P\left( Y\geqslant\dfrac{3-\mu}\sigma\rp\\
&=1-P\left( Y\leqslant\dfrac{3-\mu}\sigma\rp=0,8413\enar\]](/Generateur-Devoirs/Colles/VAC/determiner-loi-normale_c/8.png)
et donc
![\[1-\Phi(\lp\dfrac{3-\mu}\sigma\rp=\Phi(1)\]](/Generateur-Devoirs/Colles/VAC/determiner-loi-normale_c/9.png)
Comme de plus,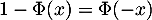 , on a donc
, on a donc
![\[\Phi(-\lp\dfrac{3-\mu}\sigma\rp=\Phi(1)\]](/Generateur-Devoirs/Colles/VAC/determiner-loi-normale_c/11.png)
et donc, à nouveau comme est bijective,
est bijective,
![\[-\dfrac{3-\mu}\sigma=1\]](/Generateur-Devoirs/Colles/VAC/determiner-loi-normale_c/13.png)
On a finalement un système de deux équations à deux inconnues à résoudre:
![\[\la\begin{array}{ll}\dfrac{9-\mu}\sigma=2\\[1em]-\dfrac{3-\mu}\sigma=1\enar\right.\]](/Generateur-Devoirs/Colles/VAC/determiner-loi-normale_c/14.png)
ou encore
![\[\la\begin{array}{ll}9-\mu=2\sigma\\\mu-3=\sigma\enar\right.\]](/Generateur-Devoirs/Colles/VAC/determiner-loi-normale_c/15.png)
d'où
![\[\la\begin{array}{ll}\mu=5\\\sigma=2\enar\right.\]](/Generateur-Devoirs/Colles/VAC/determiner-loi-normale_c/16.png)
Correction
On sait donc queOn se ramène à une loi normale centrée réduite, en posant
soit donc
Comme
De même,
![\[\begin{array}{ll}P(X\geqslant3)&=P\left( Y\geqslant\dfrac{3-\mu}\sigma\rp\\
&=1-P\left( Y\leqslant\dfrac{3-\mu}\sigma\rp=0,8413\enar\]](/Generateur-Devoirs/Colles/VAC/determiner-loi-normale_c/8.png)
et donc
Comme de plus,
et donc, à nouveau comme
On a finalement un système de deux équations à deux inconnues à résoudre:
![\[\la\begin{array}{ll}\dfrac{9-\mu}\sigma=2\\[1em]-\dfrac{3-\mu}\sigma=1\enar\right.\]](/Generateur-Devoirs/Colles/VAC/determiner-loi-normale_c/14.png)
ou encore
d'où
Tag:Variables aléatoires continues
Autres sujets au hasard:
