Théorème du rang et démonstration
Colle de mathématiques
Sujet de colle de maths:- Applications linéairesApplications linéaires
Énoncé du sujet
Énoncer et démontrer le théorème du rang pour une application linéaire entre deux espaces 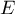 et
et 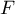 de dimensions finies.
de dimensions finies.
Correction
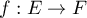 une application linéaire, alors le théorème du rang énonce que
une application linéaire, alors le théorème du rang énonce que
![\[\text{rg}(f)+\dim\lp\text{Ker}(f)\rp=\dim(E)\]](/Generateur-Devoirs/Colles/Applin/demonstration-theoreme-rang_c/2.png)
Soit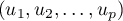 une base du noyau et
une base du noyau et
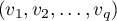 une base de l'image,
c'est-à-dire que pour tout
une base de l'image,
c'est-à-dire que pour tout  on a
on a
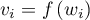 .
.
Le théorème du rang est alors équivalent à montrer que la famille
![\[\mathcal{F}=\left( u_1, u_2, \dots, u_p, w_1, w_2, \dots, w_q\rp\]](/Generateur-Devoirs/Colles/Applin/demonstration-theoreme-rang_c/7.png)
est une base de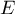 , c'est-à-dire est une famille génératrice et libre.
, c'est-à-dire est une famille génératrice et libre.
Cette famille est libre. En effet, si
![\[a_1u_1+\dots+a_pu_p+b_1w_1+\dots+b_qw_q=0\]](/Generateur-Devoirs/Colles/Applin/demonstration-theoreme-rang_c/9.png)
alors, en appliquant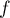 , qui est linéaire, on obtient
, qui est linéaire, on obtient
![\[a_1f\left( u_1\rp+\dots+a_pf\left( u_p\rp+b_1f\left( w_1\rp+\dots+b_qf\left( w_q\rp=0\]](/Generateur-Devoirs/Colles/Applin/demonstration-theoreme-rang_c/11.png)
or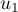 , …,
, …, 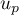 appartiennent au noyau de
appartiennent au noyau de 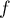 , d'où on doit avoir
, d'où on doit avoir
![\[\begin{array}{ll}&b_1f\left( w_1\rp+\dots+b_qf\left( w_q\rp=0\\[.5em]
\iff&b_1v_1+\dots+b_qv_q=0\enar\]](/Generateur-Devoirs/Colles/Applin/demonstration-theoreme-rang_c/15.png)
mais comme on est une base de l'image, en particulier cette famille est libre et on a donc nécessairement
est une base de l'image, en particulier cette famille est libre et on a donc nécessairement
![\[b_1=\dots=b_q=0\]](/Generateur-Devoirs/Colles/Applin/demonstration-theoreme-rang_c/17.png)
Maintenant, en reportant ceci dans notre relation de liaison
![\[a_1u_1+\dots+a_pu_p+b_1w_1+\dots+b_qw_q=0\]](/Generateur-Devoirs/Colles/Applin/demonstration-theoreme-rang_c/18.png)
on doit donc avoir maintenant
![\[a_1u_1+\dots+a_pu_p=0\]](/Generateur-Devoirs/Colles/Applin/demonstration-theoreme-rang_c/19.png)
mais comme est une base du noyau, donc en particulier est libre, on doit cette fois avoir nécessairement
est une base du noyau, donc en particulier est libre, on doit cette fois avoir nécessairement
![\[a_1=\dots=a_p=0\]](/Generateur-Devoirs/Colles/Applin/demonstration-theoreme-rang_c/21.png)
Tous les coefficients sont donc nécessairement nuls et la famille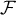 est donc libre.
est donc libre.
Cette famille est aussi génératrice. Soit en effet un élément quelconque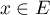 , et en décomposant dans la base de l'image
, et en décomposant dans la base de l'image
![\[\begin{array}{ll}f(x)&=\alpha_1 v_1+\dots +\alpha_q v_q\\[.5em]
&=\alpha_1 f(w_1)+\dots +\alpha_q f(w_q)\enar\]](/Generateur-Devoirs/Colles/Applin/demonstration-theoreme-rang_c/24.png)
Maintenant
![\[y=x-\lp\alpha_1w_1+\dots+\alpha_qw_q\rp\]](/Generateur-Devoirs/Colles/Applin/demonstration-theoreme-rang_c/25.png)
appartient au noyau de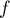 et on peut donc écrire, sur la base du noyau
et on peut donc écrire, sur la base du noyau
![\[y=\beta_1u_1+\dots+\beta_pu_p\]](/Generateur-Devoirs/Colles/Applin/demonstration-theoreme-rang_c/27.png)
soit
![\[\begin{array}{ll}x&=y+\lp\alpha_1w_1+\dots+\alpha_qw_q\rp\\[.5em]
&=\beta_1u_1+\dots+\beta_pu_p+\alpha_1w_1+\dots+\alpha_qw_q\enar\]](/Generateur-Devoirs/Colles/Applin/demonstration-theoreme-rang_c/28.png)
qui montre donc qu'un élément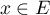 quelconque se décompose sur la famille
quelconque se décompose sur la famille
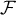 qui est donc aussi génératrice.
qui est donc aussi génératrice.
Correction
SoitSoit
Le théorème du rang est alors équivalent à montrer que la famille
est une base de
Cette famille est libre. En effet, si
alors, en appliquant
or
![\[\begin{array}{ll}&b_1f\left( w_1\rp+\dots+b_qf\left( w_q\rp=0\\[.5em]
\iff&b_1v_1+\dots+b_qv_q=0\enar\]](/Generateur-Devoirs/Colles/Applin/demonstration-theoreme-rang_c/15.png)
mais comme on
Maintenant, en reportant ceci dans notre relation de liaison
on doit donc avoir maintenant
mais comme
Tous les coefficients sont donc nécessairement nuls et la famille
Cette famille est aussi génératrice. Soit en effet un élément quelconque
![\[\begin{array}{ll}f(x)&=\alpha_1 v_1+\dots +\alpha_q v_q\\[.5em]
&=\alpha_1 f(w_1)+\dots +\alpha_q f(w_q)\enar\]](/Generateur-Devoirs/Colles/Applin/demonstration-theoreme-rang_c/24.png)
Maintenant
appartient au noyau de
soit
![\[\begin{array}{ll}x&=y+\lp\alpha_1w_1+\dots+\alpha_qw_q\rp\\[.5em]
&=\beta_1u_1+\dots+\beta_pu_p+\alpha_1w_1+\dots+\alpha_qw_q\enar\]](/Generateur-Devoirs/Colles/Applin/demonstration-theoreme-rang_c/28.png)
qui montre donc qu'un élément
Tag:Applications linéaires
Autres sujets au hasard:

Voir aussi: