Projecteurs et somme directe d'images
Colle de mathématiques
Sujet de colle de maths:- ProjecteursProjecteurs dans des espaces vectoriels
- Applications linéairesApplications linéaires
- Espace vectorielEspaces vectoriels
Énoncé du sujet
Soit  et
et 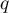 deux projecteurs d'un même espace vectoriel et vérifiant
deux projecteurs d'un même espace vectoriel et vérifiant  .
.
- Que peut-on dire de
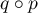 ?
?
- On note
 .
Montrer que
.
Montrer que 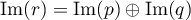 .
.
Correction
Correction
- Pour tout
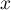 ,
,  ,
et donc, comme
,
et donc, comme 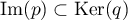 ,
on a
,
on a 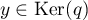 soit
soit 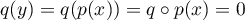 .
.
Ainsi, est l'application nulle.
est l'application nulle.
- On cherche à montrer la some directe
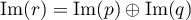 .
.
Soit , c'est-à-dire qu'il exsite
, c'est-à-dire qu'il exsite 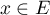 tel que
tel que
![\[\begin{array}{ll}y&=r(x)\\[.4em]
&=p(x)+q(x)-p\circ q(x)\\[.4em]
&=\underbrace{p\bigl(x-q(x)\bigr)}_{\in\text{Im}(p)}+\underbrace{q(x)}_{\in\text{Im}(q)}\enar\]](/Generateur-Devoirs/Colles/Applin/exP3.3_c/10.png)
ce qui montre que .
.
Soit maintenant, dans l'autre sens,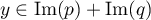 ,
c'est-à-dire qu'il existe
,
c'est-à-dire qu'il existe 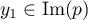 , soit
, soit 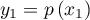 et
et 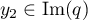 , soit
, soit  ,
tels que
,
tels que 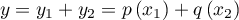 .
.
On a alors, en appliquant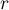 ,
,
![\[\begin{array}{lcl}r(y)&=&r\Bigl(p\left( x_1\rp+q\left( x_2\rp\Bigr)\\[.5em]
&=&r\bigl(p\left( x_1\rp\bigr)+r\bigl(q\left( x_2\rp\bigr)\\[.5em]
&=&p^2\left( x_1\rp+q\left( p\left( x_1\rp\rp-p\left( q\left( p\left( x_1\rp\rp\rp\\
&&+p\left( q\left( x_2\rp\rp+q^2\left( x_2\rp-p\left( q^2\left( x_2\rp\rp
\enar\]](/Generateur-Devoirs/Colles/Applin/exP3.3_c/19.png)
puis, en utilisant le fait que et
et 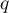 sont des projecteurs, soit
sont des projecteurs, soit 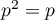 et
et  et que
et que 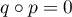 , on obtient
, on obtient
![\[\begin{array}{lcl}r(y)&=&p\left( x_1\rp+0-0\\&&+p\left( q\left( x_2\rp\rp+q\left( x_2\rp-p\left( q\left( x_2\rp\rp\\[.5em]
&=&p\left( x_1\rp+q\left( x_2\rp\\
&=&y
\enar\]](/Generateur-Devoirs/Colles/Applin/exP3.3_c/25.png)
et donc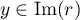 .
.
On a donc montré l'inclusion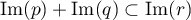 ,
et donc, finalement, l'égalite
,
et donc, finalement, l'égalite
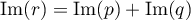 .
.
Il reste à montrer que la somme est directe.
Soit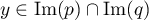 , c'est-à-dire qu'il existe
, c'est-à-dire qu'il existe
 et
et  tels que
tels que 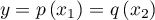 .
.
On a alors d'une part, car
d'une part, car 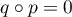 ,
et d'autre part
,
et d'autre part  , car
, car  est un projecteur.
est un projecteur.
Ainsi, et donc
et donc 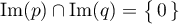 ,
alors
,
alors 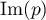 et
et 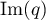 sont en somme directe:
sont en somme directe:
![\[\text{Im}(r)=\text{Im}(p)\oplus\text{Im}(q)\]](/Generateur-Devoirs/Colles/Applin/exP3.3_c/41.png)
Tags:ProjecteursApplications linéairesEspace vectoriel
Autres sujets au hasard:

Voir aussi: