Suite récurrente et série (bis)


Colle de mathématiques

Sujet de colle de maths:

Énoncé du sujet

On pose 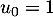$u_0=1$. Pour tout 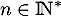$n\in\N^*$, on note
\[u_{n+1}=u_n+u_n^2\]

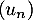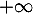  1. Montrer que la suite $(u_n)$ diverge vers $+\infty$.
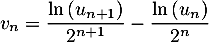  2. On pose $v_n=\dfrac{\ln\left( u_{n+1}\right)}{2^{n+1}}-\dfrac{\ln\left( u_n\right)}{2^n}$.
    Montrer que la série de terme général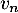 $v_n$ converge.
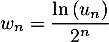  3. On pose $w_n=\dfrac{\ln\left( u_n\right)}{2^n}$.
    Montrer que la suite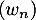 $\left( w_n\rp$ converge, on note 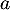$a$ sa limite.
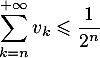  4. Montrer que $\dsp\sum_{k=n}^{+\infty}v_k\leqslant\dfrac1{2^n}$.
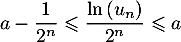  5. Montrer que $a-\dfrac1{2^n}\leqslant\dfrac{\ln\left( u_n\right)}{2^n}\leqslant a$.



Correction

Correction

Oral ENSAE - Saclay - 2019

  1. On montre par récurrence que la suite 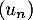$(u_n)$ est strictement positive.
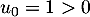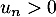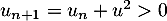    En effet $u_0=1>0$ puis, si $u_n>0$ alors $u_{n+1}=u_n+u^2>0$.

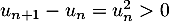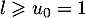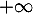    On a donc $u_{n+1}-u_n=u_n^2>0$ et cette suite est donc strictement croissante. Elle converge donc vers une limite $l\geqslant u_0=1$ ou diverge vers $+\infty$.
    Mais si elle converge vers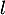 $l$, alors par passage à la limite dans la relation de récurrence, on a nécessairement
    \[l=l+l^2\iff l=0\]

    ce qui est impossible car on a vu que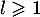 $l\geqslant1$.

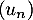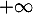    Ainsi, la suite $(u_n)$ diverge vers $+\infty$.
  2. On a
    \[\begin{array}{lcl}\ln\left( u_{n+1}\rp&=&\ln\left( u_n+u_n^2\rp\\[.5em] &=&\ln\left( u_n^2\left(1+\dfrac1{u_n}\rp\rp\\[1em] &=&2\ln\left( u_n\rp+\ln\left(1+\dfrac1{u_n}\rp \enar\]

    et donc
    \[v_n=\dfrac1{2^{n+1}}\ln\lp1+\dfrac1{u_n}\rp\]

    Or on a vu que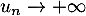 $u_n\to+\infty$, donc 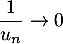$\dfrac1{u_n}\to0$ et alors
    \[v_n\underset{+\infty}{\sim}\dfrac1{2^{n+1}}\,\dfrac1{u_n}\leqslant\dfrac1{2^{n+1}}\]

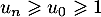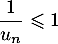    car on a vu aussi que la suite est croissante donc $u_n\geqslant u_0\geqslant1$, donc $\dfrac1{u_n}\leqslant1$.
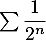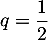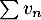    On sait de plus que la série $\sum\dfrac1{2^n}$ converge, comme une série géométrique de raison $q=\dfrac12$, et donc, par comparaison entre séries à termes positifs, $\sum v_n$ converge aussi.
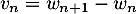  3. On a $v_n=w_{n+1}-w_n$ et donc la somme téléscopique
    \[\sum_{k=0}^n v_k= w_{n+1}-w_0\]

    et donc, puisque la série de gauche converge, il en est de même de la suite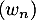 $\left( w_n\rp$.
  4. On a vu que
    \[v_n=\dfrac1{2^{n+1}}\ln\lp1+\dfrac1{u_n}\right) \leqslant\dfrac1{2^{n+1}}\ln(2)\]

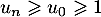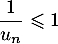    car $u_n\geqslant u_0\geqslant1$, donc $\dfrac1{u_n}\leqslant1$, et que la fonction ln est croissante.
    On a donc
    \[\sum_{k=n}^N\dfrac1{v_k} \leqslant \ln(2)\sum_{k=n}^N\dfrac1{2^{k+1}}\]

    avec
    \[\sum_{k=n}^N\dfrac1{2^{k+1}} =\dfrac1{2^{n+1}}\dfrac{1-\dfrac1{2^{N-n+1}}}{1-\dfrac12} \]

    d'où
    \[\sum_{k=n}^{+\infty}\dfrac1{2^{k+1}} =\dfrac1{2^n}\]

    On a donc trouvé que
    \[\sum_{k=n}^{+\infty}v_k\leqslant\ln(2)\dfrac1{2^n}\]

    et qui nous donne l'inégalité souhaité puisque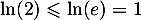 $\ln(2)\leqslant\ln(e)=1$, d'où
    \[\sum_{k=n}^{+\infty}v_k\leqslant\dfrac1{2^n}\]

  5. On a
    \[\begin{array}{lcl}\dsp\sum_{k=0}^{n-1}v_k &=&w_n-w_0\\ &=&\dfrac{\ln(u_n)}{2^{n}}-\dfrac{\ln(u_0)}{2^0}\\[.7em] &=&\dfrac{\ln(u_n)}{2^{n}} \enar\]

    car $u_0=1$.
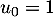    Par ailleurs
    \[\dsp\sum_{k=0}^{n-1}v_k=\sum_{k=0}^{+\infty}v_k-\sum_{k=n}^{+\infty}v_k =a-\sum_{k=n}^{+\infty}v_k \]

    d'où l'encadrement souhaité avec l'inégalité de la question précédente;


Tag:Séries

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0