Série télescopique


Colle de mathématiques

Sujet de colle de maths:

Énoncé du sujet

Montrer que la série de terme général, pour 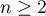$n\geq 2$,
\[u_n=\frac{1}{\sqrt{n-1}}-\frac{2}{\sqrt{n}}+\frac{1}{\sqrt{n+1}}\]

est convergente, et calculer sa somme


Correction

Correction

Il s'agit d'une série télescopique. La somme partielle s'écrit
\[\begin{array}{lcl} S_n&=&\dsp\sum_{k=2}^n \lp\dfrac1{\sqrt{k-1}}-\dfrac2{\sqrt{k}}+\dfrac1{\sqrt{k+1}}\rp\\[1.2em] &=&\dsp\sum_{k=1}^{n-1} \frac{1}{\sqrt{k}}-2\sum_{k=2}^n\dfrac1{\sqrt k}+\sum_{k=3}^{n+1} \dfrac1{\sqrt{k}}\\[1.2em] &=&1-\dfrac1{\sqrt 2}-\dfrac1{\sqrt n}+\dfrac1{\sqrt{n+1}}. \enar\]

On trouve ainsi que cette suite converge, avec pour somme
\[\lim_{n\to+\infty}S_n=1-\dfrac1{\sqrt2}\]



Tag:Séries

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0