Calcul de sommes connaissant e
Colle de mathématiques
Sujet de colle de maths:- SériesSéries
Énoncé du sujet
Sachant que 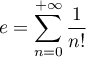 calculer les sommes
calculer les sommes
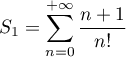 et
et
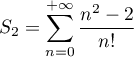 .
.
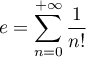 calculer les sommes
calculer les sommes
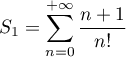 et
et
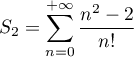 .
.
Correction
 ,
,
![\[\begin{array}{ll}\dfrac{n+1}{n!}&=\dfrac{n}{n!}+\dfrac1{n!}\\
&=\dfrac1{(n-1)!}+\dfrac1{n!}\enar\]](/Generateur-Devoirs/Colles/Series/Se_c/2.png)
et donc
![\[\begin{array}{ll}S_1&=1+\dsp\sum_{n=1}^{+\infty}\dfrac{n+1}{n!}\\
&=1+\dsp\sum_{n=1}^{+\infty}\dfrac1{(n-1)!}+\sum_{n=1}^{+\infty}\dfrac1{n!}
\enar\]](/Generateur-Devoirs/Colles/Series/Se_c/3.png)
On peut changer d'indice dans la première somme:
![\[\sum_{n=1}^{+\infty}\dfrac1{(n-1)!}
=\sum_{n=0}^{+\infty}\dfrac1{n!}=e\]](/Generateur-Devoirs/Colles/Series/Se_c/4.png)
et par ailleurs,
![\[1+\sum_{n=1}^{+\infty}\dfrac1{n!}
=\sum_{n=0}^{+\infty}\dfrac1{n!}=e\]](/Generateur-Devoirs/Colles/Series/Se_c/5.png)
On trouve finalement la somme
![\[S_1=2\]](/Generateur-Devoirs/Colles/Series/Se_c/6.png)
On procède de la même façon pour la deuxième somme:
![\[\begin{array}{ll}S_2&=\dsp\sum_{n=0}^{+\infty}\dfrac{n^2-2}{n!}\\[1.2em]
&=\dsp\sum_{n=0}^{+\infty}\dfrac{n^2}{n!}
-\sum_{n=0}^{+\infty}\dfrac2{n!}\\[1.2em]
&=\dsp\sum_{n=1}^{+\infty}\dfrac{n}{(n-1)!}
-2\sum_{n=0}^{+\infty}\dfrac1{n!}\\[1.2em]
&=\dsp\sum_{n=1}^{+\infty}\dfrac{n}{(n-1)!}-2e\enar\]](/Generateur-Devoirs/Colles/Series/Se_c/7.png)
Il reste à exprimer cette dernière somme. Pour cela on essaie de simplifier le numérateur avec le dénominateur, pour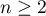 ,
,
![\[\begin{array}{ll}\dfrac{n}{(n-1)!}&=\dfrac{(n-1)+1}{(n-1)!}\\[1em]
&=\dfrac1{(n-2)!}+\dfrac1{(n-1)!}\enar\]](/Generateur-Devoirs/Colles/Series/Se_c/9.png)
et alors
![\[\sum_{n=1}^{+\infty}\dfrac{n}{(n-1)!}
=\sum_{n=2}^{+\infty}\dfrac1{(n-2)!}
+\sum_{n=1}^{+\infty}\dfrac1{(n-1)!}\]](/Generateur-Devoirs/Colles/Series/Se_c/10.png)
puis en hangeant d'indices
![\[\sum_{n=1}^{+\infty}\dfrac{n}{(n-1)!}
=\sum_{n=0}^{+\infty}\dfrac1{n!}
+\sum_{n=0}^{+\infty}\dfrac1{n!}=2e\]](/Generateur-Devoirs/Colles/Series/Se_c/11.png)
On trouve donc finalement que, simplement,
![\[S_2=0\]](/Generateur-Devoirs/Colles/Series/Se_c/12.png)
Correction
On a, pour![\[\begin{array}{ll}\dfrac{n+1}{n!}&=\dfrac{n}{n!}+\dfrac1{n!}\\
&=\dfrac1{(n-1)!}+\dfrac1{n!}\enar\]](/Generateur-Devoirs/Colles/Series/Se_c/2.png)
et donc
![\[\begin{array}{ll}S_1&=1+\dsp\sum_{n=1}^{+\infty}\dfrac{n+1}{n!}\\
&=1+\dsp\sum_{n=1}^{+\infty}\dfrac1{(n-1)!}+\sum_{n=1}^{+\infty}\dfrac1{n!}
\enar\]](/Generateur-Devoirs/Colles/Series/Se_c/3.png)
On peut changer d'indice dans la première somme:
![\[\sum_{n=1}^{+\infty}\dfrac1{(n-1)!}
=\sum_{n=0}^{+\infty}\dfrac1{n!}=e\]](/Generateur-Devoirs/Colles/Series/Se_c/4.png)
et par ailleurs,
![\[1+\sum_{n=1}^{+\infty}\dfrac1{n!}
=\sum_{n=0}^{+\infty}\dfrac1{n!}=e\]](/Generateur-Devoirs/Colles/Series/Se_c/5.png)
On trouve finalement la somme
On procède de la même façon pour la deuxième somme:
![\[\begin{array}{ll}S_2&=\dsp\sum_{n=0}^{+\infty}\dfrac{n^2-2}{n!}\\[1.2em]
&=\dsp\sum_{n=0}^{+\infty}\dfrac{n^2}{n!}
-\sum_{n=0}^{+\infty}\dfrac2{n!}\\[1.2em]
&=\dsp\sum_{n=1}^{+\infty}\dfrac{n}{(n-1)!}
-2\sum_{n=0}^{+\infty}\dfrac1{n!}\\[1.2em]
&=\dsp\sum_{n=1}^{+\infty}\dfrac{n}{(n-1)!}-2e\enar\]](/Generateur-Devoirs/Colles/Series/Se_c/7.png)
Il reste à exprimer cette dernière somme. Pour cela on essaie de simplifier le numérateur avec le dénominateur, pour
![\[\begin{array}{ll}\dfrac{n}{(n-1)!}&=\dfrac{(n-1)+1}{(n-1)!}\\[1em]
&=\dfrac1{(n-2)!}+\dfrac1{(n-1)!}\enar\]](/Generateur-Devoirs/Colles/Series/Se_c/9.png)
et alors
![\[\sum_{n=1}^{+\infty}\dfrac{n}{(n-1)!}
=\sum_{n=2}^{+\infty}\dfrac1{(n-2)!}
+\sum_{n=1}^{+\infty}\dfrac1{(n-1)!}\]](/Generateur-Devoirs/Colles/Series/Se_c/10.png)
puis en hangeant d'indices
![\[\sum_{n=1}^{+\infty}\dfrac{n}{(n-1)!}
=\sum_{n=0}^{+\infty}\dfrac1{n!}
+\sum_{n=0}^{+\infty}\dfrac1{n!}=2e\]](/Generateur-Devoirs/Colles/Series/Se_c/11.png)
On trouve donc finalement que, simplement,
Tag:Séries
Autres sujets au hasard:

Voir aussi: