Étude de la convergence de la série
Colle de mathématiques
Sujet de colle de maths:- SériesSéries
Énoncé du sujet
Monter que pour tout 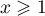 ,
, 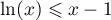 .
.
En déduire la nature de la série de terme général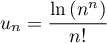
En déduire la nature de la série de terme général
Correction
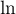 et le fait que
et le fait que 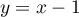 est l'équation de la tangente sa courbe en 1.
est l'équation de la tangente sa courbe en 1.
On peut aussi simplement éudier la fonction différence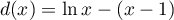 , dérivable sur
, dérivable sur  et dont la dérivée
est
et dont la dérivée
est 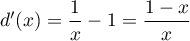 .
.
Ainsi, pour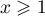 , on a
, on a 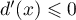 et
et 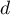 est décroissante, donc,
pour tout
est décroissante, donc,
pour tout 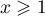 ,
, 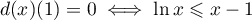 .
.
Là aussi, on peut étudier la nature de la série de diverses façons (entre autres avec la règle de d'Alembert).
Néanmoins si on se laisse guider par l'énoncé, les termes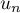 sont positifs et tels que
sont positifs et tels que
![\[u_n=\dfrac{\ln\left( n^n\right)}{n!}=\dfrac{n\ln n}{n!}=\dfrac{\ln n}{(n-1)!}\]](/Generateur-Devoirs/Colles/Series/excvg9_c/12.png)
puis, en utilisant la première inégalité,
![\[u_n\leqslant\dfrac{n-1}{(n-1)!}=\dfrac{1}{(n-2)!}\]](/Generateur-Devoirs/Colles/Series/excvg9_c/13.png)
qui est le terme général d'une série convergente. Ainsi, la série de terme général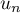 est aussi convergente.
est aussi convergente.
Correction
On peut montrer cette inégalité de plusieurs façons, avec divers outils, par exemple en utilisant la convexité de la fonctionOn peut aussi simplement éudier la fonction différence
Ainsi, pour
Là aussi, on peut étudier la nature de la série de diverses façons (entre autres avec la règle de d'Alembert).
Néanmoins si on se laisse guider par l'énoncé, les termes
puis, en utilisant la première inégalité,
qui est le terme général d'une série convergente. Ainsi, la série de terme général
Tag:Séries
Autres sujets au hasard:

Voir aussi: