Série multiple de e
Colle de mathématiques
Sujet de colle de maths:- SériesSéries
Énoncé du sujet
Soit un entier 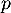 et la série
et la série 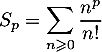 .
.
Montrer que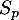 converge et que
converge et que 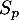 est un multiple de
est un multiple de 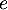 .
.
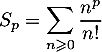 .
.Montrer que
Correction
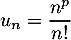 le terme général de la série, alors
le terme général de la série, alors
![\[\begin{array}{ll}\dfrac{u_{n+1}}{u_n}&=\dfrac{(n+1)^p}{(n+1)!}\tm\dfrac{n!}{n^p}\\[1.2em]
&=\lp\dfrac{n+1}n\rp^n\tm\dfrac{n!}{(n+1)!}\\[1.2em]
&=\lp1+\dfrac1n\rp^p\tm\dfrac1{n+1}
\enar\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/2.png)
et on a donc, pour tout entier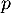 ,
,
![\[\lim_{n\to+\infty}\dfrac{u_{n+1}}{u_n}=0\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/4.png)
ce qui montre que la série de terme général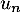 converge.
converge.
On reconnaît, pour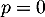 la série exponentielle:
la série exponentielle:
![\[S_0=\sum_{n\geqslant0}\dfrac1{n!}=e\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/7.png)
tandis que pour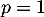 , on
, on
![\[S_1=\sum_{n\geqslant0}\dfrac{n}{n!}
=\sum_{n\geqslant1}\dfrac1{(n-1)!}\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/9.png)
et donc, avec un changement d'indice, on trouve aussi que
![\[S_1=\sum_{n\geqslant0}\dfrac1{n!}=e\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/10.png)
Ces observations peuvent nous inciter à chercher à démontrer le résultat par récurrence. La propriété "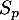 est un multiple de
est un multiple de 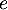 " est donc initialisée.
" est donc initialisée.
Hérédité: supposons que pour un entier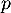 on ait que pour tout entier
on ait que pour tout entier 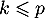 la série
la série 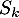 est un multiple de
est un multiple de 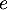 , c'est-à-dire
, c'est-à-dire 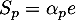 avec
avec 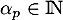 .
.
On cherche alors à montrer que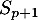 est encore un multiple de
est encore un multiple de 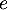 .
.
![\[S_{p+1}=\sum_{n\geqslant0}\dfrac{n^{p+1}}{n!}
=\sum_{n\geqslant1}\dfrac{n^p}{(n-1)!}\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/21.png)
On change d'indice pour obtenir
![\[S_{p+1}=\sum_{n\geqslant0}\dfrac{(n+1)^p}{n!}\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/22.png)
En utilisant la formule du binôme de Newton, on a alors
![\[S_{p+1}=\sum_{n\geqslant0}\dfrac{\dsp\sum_{k=0}^p\binom{k}{p}n^k}{n!}\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/23.png)
soit encore,
![\[\begin{array}{ll}S_{p+1}&=\dsp\sum_{k=0}^p\binom{p}{k}\sum_{n\geqslant0}\dfrac{n^k}{n!}\\[1.2em]
&=\dsp\sum_{k=0}^p\binom{p}{k}S_k\\[1.2em]
&=\dsp\sum_{k=0}^p\binom{p}{k}\alpha_ke\\[1.2em]
&=e\dsp\sum_{k=0}^p\binom{p}{k}\alpha_k
\enar\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/24.png)
Or les coefficients binomiaux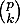 sont des nombres entiers (c'est le nombre de façons de choisir
sont des nombres entiers (c'est le nombre de façons de choisir 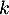 éléments dans un ensemble de
éléments dans un ensemble de 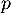 éléments) et les coefficeint
éléments) et les coefficeint 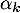 aussi, ainsi on a trouvé que
aussi, ainsi on a trouvé que
![\[S_{p+1}=\alpha_{p+1}e\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/29.png)
avec
![\[\alpha_{p+1} = \sum_{k=0}^p\binom{k}{p}\alpha_k \in\N\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/30.png)
On vient donc de démontrer, d'après le principe de récurrence, la propriété: pour tout entier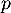 la série
la série 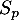 est un multiple de
est un multiple de 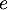 .
.
Correction
On montre la converge de la série en utilisant le critère de d'Alembert. Soit![\[\begin{array}{ll}\dfrac{u_{n+1}}{u_n}&=\dfrac{(n+1)^p}{(n+1)!}\tm\dfrac{n!}{n^p}\\[1.2em]
&=\lp\dfrac{n+1}n\rp^n\tm\dfrac{n!}{(n+1)!}\\[1.2em]
&=\lp1+\dfrac1n\rp^p\tm\dfrac1{n+1}
\enar\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/2.png)
et on a donc, pour tout entier
ce qui montre que la série de terme général
On reconnaît, pour
![\[S_0=\sum_{n\geqslant0}\dfrac1{n!}=e\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/7.png)
tandis que pour
![\[S_1=\sum_{n\geqslant0}\dfrac{n}{n!}
=\sum_{n\geqslant1}\dfrac1{(n-1)!}\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/9.png)
et donc, avec un changement d'indice, on trouve aussi que
![\[S_1=\sum_{n\geqslant0}\dfrac1{n!}=e\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/10.png)
Ces observations peuvent nous inciter à chercher à démontrer le résultat par récurrence. La propriété "
Hérédité: supposons que pour un entier
On cherche alors à montrer que
![\[S_{p+1}=\sum_{n\geqslant0}\dfrac{n^{p+1}}{n!}
=\sum_{n\geqslant1}\dfrac{n^p}{(n-1)!}\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/21.png)
On change d'indice pour obtenir
![\[S_{p+1}=\sum_{n\geqslant0}\dfrac{(n+1)^p}{n!}\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/22.png)
En utilisant la formule du binôme de Newton, on a alors
![\[S_{p+1}=\sum_{n\geqslant0}\dfrac{\dsp\sum_{k=0}^p\binom{k}{p}n^k}{n!}\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/23.png)
soit encore,
![\[\begin{array}{ll}S_{p+1}&=\dsp\sum_{k=0}^p\binom{p}{k}\sum_{n\geqslant0}\dfrac{n^k}{n!}\\[1.2em]
&=\dsp\sum_{k=0}^p\binom{p}{k}S_k\\[1.2em]
&=\dsp\sum_{k=0}^p\binom{p}{k}\alpha_ke\\[1.2em]
&=e\dsp\sum_{k=0}^p\binom{p}{k}\alpha_k
\enar\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/24.png)
Or les coefficients binomiaux
avec
![\[\alpha_{p+1} = \sum_{k=0}^p\binom{k}{p}\alpha_k \in\N\]](/Generateur-Devoirs/Colles/Series/multiple-e_c/30.png)
On vient donc de démontrer, d'après le principe de récurrence, la propriété: pour tout entier
Tag:Séries
Autres sujets au hasard:

Voir aussi: