Logarithme et série télescopique

Colle de mathématiques

Sujet de colle de maths:

SériesSéries

Énoncé du sujet

Donner la nature de la série, puis calculer sa valeur,

$\sum_{n=2}^{\infty}\ln\lp1-\dfrac1{n^2}\rp$

Correction

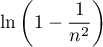$\dsp\ln\lp1-\dfrac1{n^2}\rp$ est de signe constant, négatif, et on a l'équivalent

$\ln\lp1-\dfrac1{n^2}\rp\sim-\dfrac1{n^2}$

qui est le terme général d'une série de Riemann convergente (avec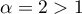 $\alpha=2>1$ ). On a de plus,

$\sum_{n=2}^N\ln\lp1-\dfrac1{n^2}\right) =\ln\lp\prod_{n=2}^N\lp1-\dfrac1{n^2}\rp\rp$

avec le produit, qui s'avère télescopique après avoir écrit chaque terme sur une fraction et remarqué l'identité remarquable:

$\begin{array}{ll}\dsp\prod_{n=2}^N\lp1-\dfrac1{n^2}\right) &=\lp1-\dfrac1{2^2}\rp\lp1-\dfrac1{3^2}\rp\lp1-\dfrac1{4^2}\rp \dots\lp1-\dfrac1{N^2}\rp\\[1em] &=\dfrac{2^2-1}{2^2}\tm\dfrac{3^2-1}{3^2}\tm\dfrac{4^2-1}{4^2}\dots\tm\dfrac{N^2-1}{N^2}\\[1em] &=\dfrac{1\tm3}{2^2}\tm\dfrac{2\tm4}{3^2}\tm\dfrac{3\tm5}{4^2}\tm\dots\tm\dfrac{(N-1)(N+1)}{N^2}\\[.8em] &=\dfrac12\tm\dfrac{N+1}N \enar$

On obtient ainsi,

$\sum_{n=2}^N\ln\lp1-\dfrac1{n^2}\rp=\ln\lp\dfrac{N+1}{2N}\rp$

et donc

$\begin{array}{ll}\dsp\sum_{n=2}^{+\infty}\ln\lp1-\dfrac1{n^2}\right) &=\dsp\lim_{N\to+\infty}\sum_{n=2}^N\ln\lp1-\dfrac1{n^2}\rp\\[1.4em] &=\ln\lp\dfrac12\rp=-\ln(2)\enar$

Tag:Séries

Autres sujets au hasard:

Voir aussi: