Rolle et polynômes
Colle de mathématiques
Sujet de colle de maths:- PolynômePolynômes
- Rolle - AFThéorème de Rolle et théorème des accroissements finis
Énoncé du sujet
Soit 
un polynôme de ![$\R[X]$](/Generateur-Devoirs/Colles/Polynomes/exPolynome-Rolle-racines-reelles/2.png)
qui dont toutes les racines sont simples.
Montrer que toutes les racines de
sont aussi simples.
un polynôme de qui dont toutes les racines sont simples.
Montrer que toutes les racines de
sont aussi simples.
Correction
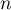, qui admet donc 
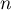racines réelles.
Si toutes les racines 
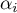de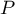 
sont simples et distinctes:
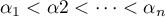alors, en appliquant le théorème de Rolle 
fois à la fonction polynôme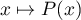 
dérivable sur 
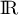donc sur chaque intervalle 
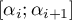, on obtient 
racines réelles distinctes, car elles appartiennent toutes à des intervalles disjoints ![$]\alpha_i;\alpha_{i+1}[$](/Generateur-Devoirs/Colles/Polynomes/exPolynome-Rolle-racines-reelles_c/11.png)
, pour 
.
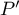Il reste à étudier le cas où des racines sont multiples. Supposons maintenant que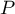
admettent 
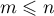racines réelles distinctes, chacune de multiplicité
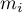avec
![\[\sum_{i=1}^mm_i=n\]](/Generateur-Devoirs/Colles/Polynomes/exPolynome-Rolle-racines-reelles_c/16.png)
D'une part, chaque racine de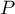
de multiplicité 
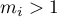est aussi racine de 
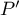de multiplicité 
,
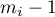et d'autre part, le théorème de Rolle nous fournit aussi 
autres racines réelles distinctes pour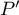 
.
Le nombre de racine réelles de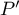
est donc
![\[\begin{array}{ll}m-1+\dsp\sum_{i=1}^m\left( m_i-1\right)
&=m-1+\dsp\sum_{i=1}^mm_i-\sum_{i=1}^m1\\
&=m-1+n-m\\
&=n-1\enar\]](/Generateur-Devoirs/Colles/Polynomes/exPolynome-Rolle-racines-reelles_c/24.png)
On a donc toutes les racines de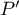
qui sont donc bien toutes réelles.
Correction
On considère un polynôme de degré, qui admet donc racines réelles.
Si toutes les racines de sont simples et distinctes:
alors, en appliquant le théorème de Rolle fois à la fonction polynôme dérivable sur donc sur chaque intervalle , on obtient racines réelles distinctes, car elles appartiennent toutes à des intervalles disjoints , pour .
Il reste à étudier le cas où des racines sont multiples. Supposons maintenant que
admettent racines réelles distinctes, chacune de multiplicité
avec
D'une part, chaque racine de
de multiplicité est aussi racine de de multiplicité ,
et d'autre part, le théorème de Rolle nous fournit aussi autres racines réelles distinctes pour .
Le nombre de racine réelles de
est donc
On a donc toutes les racines de
qui sont donc bien toutes réelles.
Tags:PolynômeRolle - AF
Autres sujets au hasard:
Voir aussi: