Résolution d'une équation différentielle à l'aide d'un développement en série entière
Colle de mathématiques
Sujet de colle de maths:- Séries entièresSéries entières
- Équation différentielleÉquation différentielle
Énoncé du sujet
On considère l'équation différentielle
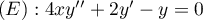 où
où  désigne la fonction inconnue supposée deux fois dérivables.
désigne la fonction inconnue supposée deux fois dérivables.
- Chercher une solution développable en série entière.
- Résoudre directement
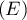 en effectuant le changement de variable
en effectuant le changement de variable 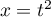 pour
pour 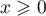 .
.
Correction
 où
où 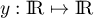 désigne la fonction inconnue supposée deux fois dérivable.
désigne la fonction inconnue supposée deux fois dérivable.
Correction
On considère l'équation différentielle- On suppose que
 est développable en série entière, dont on précisera le rayon de convergence
est développable en série entière, dont on précisera le rayon de convergence  ultérieurement et on supposera que
ultérieurement et on supposera que 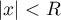 par la suite,
par la suite,
![\[y(x)=\sum_{n\geqslant0}a_nx^n\]](/Generateur-Devoirs/Colles/SeriesEnt/exEqDiffSE1_c/6.png)
alors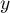 est dérivable, terme à terme pour
est dérivable, terme à terme pour  et
et
![\[y'(x)=\sum_{n\geqslant1}na_nx^{n-1}\]](/Generateur-Devoirs/Colles/SeriesEnt/exEqDiffSE1_c/9.png)
et
![\[y''(x)=\sum_{n\geqslant2}n(n-1)a_nx^{n-2}\]](/Generateur-Devoirs/Colles/SeriesEnt/exEqDiffSE1_c/10.png)
On a alors
![\[\begin{array}{llcl}&4xy''+2y'-y=0\\[.5em]
\iff&\dsp\sum_{n\geqslant2}4n(n-1)a_nx^{n-1}
+\sum_{n\geqslant1}2na_nx^{n-1}
-\sum_{n\geqslant0}a_nx^n&=&0\\[.8em]
\iff&\dsp\lp-a_0+2a_1\rp+\sum_{n\geqslant2}\Bigl(4n(n-1)a_n+2na_n-a_{n-1}\Bigr)x^{n-1}&=&0
\enar\]](/Generateur-Devoirs/Colles/SeriesEnt/exEqDiffSE1_c/11.png)
d'où on tire: puis, pour tout entier
puis, pour tout entier 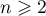 ,
,
![\[4n(n-1)a_n+2na_n-a_{n-1}=0\]](/Generateur-Devoirs/Colles/SeriesEnt/exEqDiffSE1_c/14.png)
ou encore
![\[a_n=\dfrac1{2n\left( 2n-1\right)}a_{n-1}\]](/Generateur-Devoirs/Colles/SeriesEnt/exEqDiffSE1_c/15.png)
On trouve alors, par une récurrence immédiate
![\[\begin{array}{ll}a_n&=\dfrac1{2n\left( 2n-1\right)}a_{n-1}\\[.8em]
&=\dfrac1{2n\left( 2n-1\right)}\tm\dfrac1{2(n-1)(2n-3)}a_{n-2}\\[.8em]
&=\dfrac1{2n\left( 2n-1\right)}\tm\dfrac1{(2n-2))(2n-3)}a_{n-2}\\[.8em]
&= \ \dots \\[.5em]
&=\dfrac{2}{(2n)!}a_1\\[.8em]
&=\dfrac1{(2n)!}a_0\enar\]](/Generateur-Devoirs/Colles/SeriesEnt/exEqDiffSE1_c/16.png)
Ainsi,
![\[y(x)=a_0\sum_{n\geqslant2}\dfrac1{(2n)!}x^n\]](/Generateur-Devoirs/Colles/SeriesEnt/exEqDiffSE1_c/17.png)
On peut exprimer cette série à l'aide de fonctions usuelles: c'est le développement du cosinus hyperbolique.
On retrouve aussi cela à partir du développement de l'exponentielle: ici seuls les termes pairs sont présents:
![\[\sum_{n\geqslant2}\dfrac1{(2n)!}x^n
=\dfrac12\lp\sum_{n\geqslant2}\dfrac{(\sqrt{x})^n}{n!}
+\sum_{n\geqslant2}\dfrac{(-\sqrt{x})^n}{n!}\right)
\]](/Generateur-Devoirs/Colles/SeriesEnt/exEqDiffSE1_c/18.png)
et ainsi,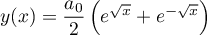 .
.
Enfin, le rayon de convergence est infini, ce qui justifie, a posteriori les calculs effectués (dérivabilité de la série, et drivation terme à terme).
Réciproquement, on vérifie bien que cette fonction est solution de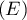 .
.
- Soit
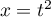 et
et 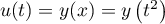 ,
alors
,
alors 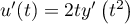 ,
puis
,
puis 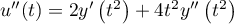 .
.
Ainsi,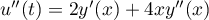 ,
et on a donc, d'après
,
et on a donc, d'après  ,
,
 ,
équation qui se résout facilement en
,
équation qui se résout facilement en
 .
.
On en déduit que .
.
Tags:Séries entièresÉquation différentielle
Autres sujets au hasard:

Voir aussi: