Discrétisation d'une équation différentielle
Colle de mathématiques
Sujet de colle de maths:- SuitesSuites
- Équation différentielleÉquation différentielle
Énoncé du sujet
On considère deux réels 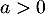 et
et 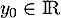 fixés,
ainsi qu'une fonction
fixés,
ainsi qu'une fonction 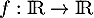 qui vérifie les propriétés suivantes:
qui vérifie les propriétés suivantes:
![\[\la\begin{array}{l}
\forall t\in\R, f'(t)=-af(t)\\
f(0)=y_0
\enar\right.\]](/Generateur-Devoirs/Colles/Suites/eqdiff/4.png)
- On pose
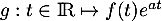 .
.
- Calculer la dérivée
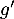 de
de 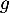 .
.
- En déduire l'expression de
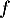 .
.
- Calculer la dérivée
- On fixe un réel
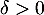 et on introduit la suite
et on introduit la suite 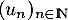 définie par
définie par
![\[u_0=y_0 \qquad\text{et}\qquad \forall n\geqslant0,\ u_{n+1}=u_n-a\delta u_n\]](/Generateur-Devoirs/Colles/Suites/eqdiff/11.png)
- Trouver une condition nécessaire et suffisante pour que
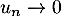 lorsque
lorsque 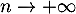 .
.
- Trouver une condition nécessaire et suffisante pour que
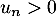 pour tout
pour tout 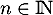 .
.
- Trouver une condition nécessaire et suffisante pour que
- On suppose dorénavant que cette dernière condition est vérfiée
et on considère la suite
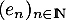 définie par
définie par
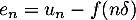 .
.
- Montrer que
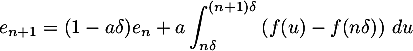 .
.
- En déduire que
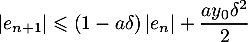 .
.
- Montrer que
Correction
Correction
Oral ENS ULM - 2021-
-
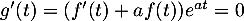
-
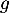 est donc constante,
est donc constante, 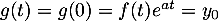 donc
donc 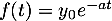 .
.
-
-
- On a
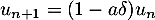 , et cette suite est donc une suite géométrique de raison
, et cette suite est donc une suite géométrique de raison 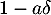 . Donc
. Donc 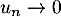 si et seulement si
si et seulement si 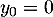 ou
ou 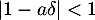 .
.
-
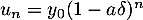 . Donc
. Donc 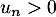 pour tout
pour tout 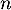 si et seulement si
si et seulement si  et
et 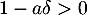 .
.
- On a
-
- D'une part,
![\[\begin{array}{ll}
e_{n+1}&=u_{n+1}-f((n+1)\delta)\\[.4em]
&=(1-a\delta)u_n-f((n+1)\delta)\\[.4em]
&=(1-a\delta)e_n+(1-a\delta)f(n\delta)-f((n+1)\delta)\enar\]](/Generateur-Devoirs/Colles/Suites/eqdiff_c/15.png)
D'autre part, l'intégrale proposée dans l'énoncé se réécrit
![\[\begin{array}{ll}a\dsp\int_{n\delta}^{(n+1)\delta} (f(u)-f(n\delta))\,du
&=\dsp\int_{n\delta}^{(n+1)\delta} af(u)\,du-af(n\delta)\int_{n\delta}^{(n+1)\delta} du\\[1em]
&=\dsp\int_{n\delta}^{(n+1)\delta} -f'(u)\,du-a\delta f(n\delta)\\[1em]
&=-f((n+1)\delta)+f(n\delta)-a\delta f(n\delta)\\[.7em]
&=(1-a\delta)f(n\delta)-f((n+1)\delta)
\enar\]](/Generateur-Devoirs/Colles/Suites/eqdiff_c/16.png)
Donc on a bien finalement
![\[e_{n+1}=(1-a\delta)e_n+a\int_{n\delta}^{(n+1)\delta} (f(u)-f(n\delta))\,du\]](/Generateur-Devoirs/Colles/Suites/eqdiff_c/17.png)
- D'après l'inégalité triangulaire, on a la majoration
![\[|e_{n+1}|\le (1-a\delta)|e_n|+a\int_{n\delta}^{(n+1)\delta} |f(u)-f(n\delta)|\,du\]](/Generateur-Devoirs/Colles/Suites/eqdiff_c/18.png)
Le théorème des accroisssements finis permet alors de majorer le terme à intégrer: il existe![$\alpha\in]n\delta; (n+1)\delta[$](/Generateur-Devoirs/Colles/Suites/eqdiff_c/19.png) tel que
tel que
![\[|f(u)-f(n\delta)|=|f'(\alpha)(u-n\delta)|\]](/Generateur-Devoirs/Colles/Suites/eqdiff_c/20.png)
avec, comme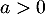 et
et  ,
,
![\[|f'(\alpha)|=|af(\alpha)|=ay_0e^{-a\alpha}\leqslant ay_0\]](/Generateur-Devoirs/Colles/Suites/eqdiff_c/23.png)
et on obtient donc, pour![$u\in[n\delta; (n+1)\delta]$](/Generateur-Devoirs/Colles/Suites/eqdiff_c/24.png) on a
on a
![\[|f(u)-f(n\delta)|\leqslant ay_0(u-n\delta)|\]](/Generateur-Devoirs/Colles/Suites/eqdiff_c/25.png)
d'où
![\[\begin{array}{ll}\dsp\int_{n\delta}^{(n+1)\delta}|f(u)-f(n\delta)|\,du
&\leqslant ay_0\dsp\int_{n\delta}^{(n+1)\delta}(u-n\delta)\,du\\[1em]
&=ay_0\lb\dfrac{(u-n\delta)^2}2\rb_{n\delta}^{(n+1)\delta}\\[1.2em]
&=ay_0\dfrac{\delta^2}2\enar\]](/Generateur-Devoirs/Colles/Suites/eqdiff_c/26.png)
et on obtient ainsi l'inégalité demandée.
- D'une part,
Tags:SuitesÉquation différentielle
Autres sujets au hasard:

Voir aussi: