Représentation paramétrique de droites et droite perpendiculaire à deux autres
Colle de mathématiques
Sujet de colle de maths:- Géométrie dans l'espaceGéométrie dans l'espace
Énoncé du sujet
Dans l'espace muni d'un repère orthonormé
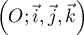 ,
on considère les droites
,
on considère les droites
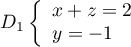 et
et
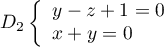
- Donner un système d'équations paramétriques des droites
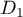 et
et 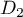 .
.
- Déterminer un système d'équations paramétriques
de la droite
 perpendiculaire commune à
perpendiculaire commune à
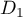 et
et 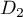 .
.
Correction
Correction
- On prend par exemple
 comme paramètre, et alors pour
comme paramètre, et alors pour  ,
,
![\[\begin{array}{rl}D_1&\la\begin{array}{ll}x+t=2\\y=-1\\z=t\enar\right.,t\in\R\\[2em]
\iff&\la\begin{array}{ll}x=2-t\\y=-1\\z=t\enar\right.,t\in\R\enar\]](/Generateur-Devoirs/Colles/Geom3D/ex4_c/3.png)
et de même pour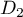 ,
,
![\[\begin{array}{rl}D_2&\la\begin{array}{ll} y-t+1=0\\x+t=0\\z=t\enar\right.,t\in\R\\[2em]
\iff&\la\begin{array}{ll} x=-t\\y=-1+t\\z=t\enar\right.,t\in\R\enar\]](/Generateur-Devoirs/Colles/Geom3D/ex4_c/5.png)
- Un vecteur directeur
 de
de 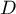 vérifie
vérifie  où
où 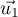 et
et 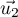 sont des vecteurs directeurs de
sont des vecteurs directeurs de 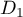 et
et 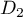 .
.
À l'aide des représentations paramétriques précédentes, on a et
et 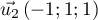 et donc
et donc 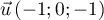 .
.
Il suffit maintenant de trouver un point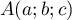 de
de 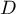 et la représentation paramétrique de
et la représentation paramétrique de 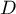 :
:
![\[\la\begin{array}{ll}x=a-t\\y=b\\z=c-t\enar\right.,t\in\R\]](/Generateur-Devoirs/Colles/Geom3D/ex4_c/19.png)
Comme ,
, 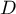 et
et 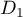 sont sécantes en
sont sécantes en 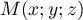 :
il existe des réels
:
il existe des réels 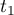 et
et 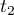 tels que
tels que
![\[\la\begin{array}{lclcl} x&=&2-t_1&=&a-t_2\\y&=&-1&=&b\\z&=&t_1&=&c-t_2\enar\right.\]](/Generateur-Devoirs/Colles/Geom3D/ex4_c/26.png)
et de même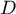 et
et 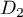 sont sécantes en
sont sécantes en 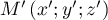 :
il existe des réels
:
il existe des réels  et
et 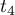 tels que
tels que
![\[\la\begin{array}{lclcl} x'&=&-t_3&=&a-t_4\\y'&=&-1+t_3&=&b\\z'&=&t_3&=&c-t_4\enar\right.\]](/Generateur-Devoirs/Colles/Geom3D/ex4_c/32.png)
On a donc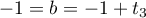 soit
soit 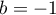 et
et 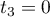 .
.
Comme , on a aussi
, on a aussi  donc
donc  et
et  donc
donc 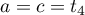 .
.
Il nous reste maintenant 2 équations à exploiter:
![\[\la\begin{array}{lclcl} x&=&2-t_1&=&a-t_2\\z&=&t_1&=&c-t_2\enar\right.\]](/Generateur-Devoirs/Colles/Geom3D/ex4_c/41.png)
soit
![\[\la\begin{array}{ll} 2-t_1=a-t_2\\t_1=a-t_2\enar\right.
\iff\la\begin{array}{ll} -t_1+t_2=a-2\\t_1+t_2=a\enar\right.\]](/Generateur-Devoirs/Colles/Geom3D/ex4_c/42.png)
Le déterminant de ce système est non nul, et donc pour tout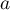 on trouve une unique solution pour
on trouve une unique solution pour 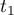 et
et  .
.
Ainsi, tout point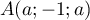 , pour tout réel
, pour tout réel  convient, par exemple
convient, par exemple 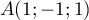 et alors
et alors
![\[\la\begin{array}{ll}x=1-t\\y=-1\\z=1-t\enar\right.,t\in\R\]](/Generateur-Devoirs/Colles/Geom3D/ex4_c/49.png)
est une représentation paramétrique de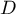 .
.
Tag:Géométrie dans l'espace
Autres sujets au hasard:

Voir aussi: