Réciproque d'une fonction de répartition
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires continuesVariables aléatoires continues
Énoncé du sujet
Oral ESCP, BL - 2021
Soit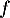 la fonction définie sur R par, pour tout réel
la fonction définie sur R par, pour tout réel 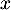 ,
,
![\[f(x)=\dfrac2{\left( e^x+e^{-x}\rp^2}\]](/Generateur-Devoirs/Colles/VAC/ESCP-BL-2021-4.7/3.png)
Soit
- Montrer que
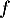 peut être considérée comme une densité d'une certaine variable aléatoire
peut être considérée comme une densité d'une certaine variable aléatoire  .
.
-
- Montrer que
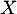 possède une espérance et donner sa valeur.
possède une espérance et donner sa valeur.
- Montrer que
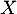 possède une variance (on ne demande pas sa valeur).
possède une variance (on ne demande pas sa valeur).
- On note
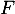 la fonction de répartition de
la fonction de répartition de 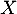 . Montrer, sans calculer
. Montrer, sans calculer 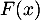 , que
, que  est une bijection de
est une bijection de  dans un intervalle
dans un intervalle 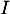 que l’on précisera.
que l’on précisera.
- Montrer que
- On considère la variable aléatoire
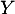 définie par
définie par 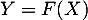 .
.
- Déterminer la loi de
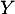 .
.
- Calculer l'expression de
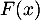 pour tout réel
pour tout réel 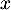 .
.
- Déterminer
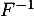 , bijection réciproque de
, bijection réciproque de 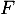 .
.
- Déterminer la loi de
Correction
Correction
Oral ESCP, BL - 2021-
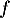 est clairement positive et continue sur
est clairement positive et continue sur 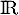 .
De plus, pour
.
De plus, pour 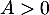 ,
,
![\[\begin{array}{ll}\dsp\int_{-A}^A f(x)dx
&=\dsp\int_{-A}^A\dfrac2{\left( e^x+e^{-x}\rp^2}dx\\
&=\dsp\int_{-A}^A\dfrac{2e^{2x}}{e^{2x}\left( e^x+e^{-x}\rp^2}dx\\
&=\dsp\int_{-A}^A\dfrac{2e^{2x}}{\left( e^{2x}+1\rp^2}dx\\
&=\lb\dfrac{-1}{e^{2x}+1}\rb_{-A}^A\\
&=-\dfrac1{e^{2A}+1}+\dfrac1{e^{-2A}+1}
\enar\]](/Generateur-Devoirs/Colles/VAC/ESCP-BL-2021-4.7_c/4.png)
et on trouve donc, à la limite où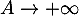 ,
,
![\[\int_{-\infty}^{+\infty}f(t)dt=1\]](/Generateur-Devoirs/Colles/VAC/ESCP-BL-2021-4.7_c/6.png)
ce qui finit de montrer que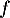 peut bien être considérée comme une densité de probabilité.
peut bien être considérée comme une densité de probabilité.
- On a
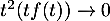 lorsque
lorsque 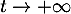 , par croissances comparées, ce qui montre, par comparaison avec une intégrale de Riemann, que
, par croissances comparées, ce qui montre, par comparaison avec une intégrale de Riemann, que 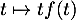 est intégrable en l'infini, et donc que
est intégrable en l'infini, et donc que 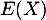 existe.
existe.
De plus, comme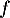 est paire, on en déduit que
est paire, on en déduit que 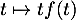 est impaire, et alors que
est impaire, et alors que 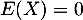 .
.
- De même que précédemment,
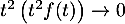 lorsque
lorsque 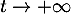 et donc
et donc 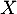 admet aussi un moment d'ordre 2 (et des moments de tout ordre, de la même façon), et en particulier,
admet aussi un moment d'ordre 2 (et des moments de tout ordre, de la même façon), et en particulier, 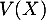 existe.
existe.
- On sait que
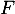 est une fonction continue, strictement croissante sur
est une fonction continue, strictement croissante sur 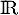 avec
avec
![\[\lim_{x\to-\infty}F(x)=0\]](/Generateur-Devoirs/Colles/VAC/ESCP-BL-2021-4.7_c/21.png)
et
![\[\lim_{x\to+\infty}F(x)=1\]](/Generateur-Devoirs/Colles/VAC/ESCP-BL-2021-4.7_c/22.png)
et ainsi,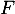 est une bijection de
est une bijection de 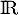 dans
dans ![$]0;1[$](/Generateur-Devoirs/Colles/VAC/ESCP-BL-2021-4.7_c/25.png) .
.
(et ceci est vrai pour tout fonction de répartition).
-
- On a
![$Y(\Omega)=]0;1[$](/Generateur-Devoirs/Colles/VAC/ESCP-BL-2021-4.7_c/26.png) . On s'intéresse à la fonction de répartition de
. On s'intéresse à la fonction de répartition de 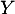 , pour
, pour ![$x\in]0;1[$](/Generateur-Devoirs/Colles/VAC/ESCP-BL-2021-4.7_c/28.png) ,
,
![\[F_Y(x)=P(Y\leqslant x)
=P(F(X)\leqslant x)\]](/Generateur-Devoirs/Colles/VAC/ESCP-BL-2021-4.7_c/29.png)
Comme, d'après la question précédente,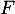 est bijective, on peut utiliser sa réciproque
est bijective, on peut utiliser sa réciproque 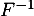 , et alors
, et alors
![\[F_Y(x)=P(X\leqslant F^{-1}(x))\]](/Generateur-Devoirs/Colles/VAC/ESCP-BL-2021-4.7_c/32.png)
et donc, en revenant à la fonction de répartition de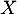 ,
,
![\[F_Y(x)=F\left( F^{-1}(x)\rp=x\]](/Generateur-Devoirs/Colles/VAC/ESCP-BL-2021-4.7_c/34.png)
On en déduit que la desnité de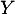 est constante sur
est constante sur ![$]0;1[$](/Generateur-Devoirs/Colles/VAC/ESCP-BL-2021-4.7_c/36.png) : il s'agit de la loi uniforme.
: il s'agit de la loi uniforme.
- On a déjà vu le calcul à la première question:
![\[\begin{array}{ll}F(x)&=\dsp\int_{-\infty}^xf(t)dt\\
&=\lb\dfrac{-1}{e^{2x}+1}\rb_{-\infty}^x\\
&=1-\dfrac1{e^{2x}+1}
\enar\]](/Generateur-Devoirs/Colles/VAC/ESCP-BL-2021-4.7_c/37.png)
- Pour déterminer l'expression de la fonction réciproque, on cherche à inverser la relation
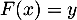
![\[\begin{array}{rl}F(x)&=1-\dfrac1{e^{2x}+1}=y\\
\iff&\dfrac1{e^{2x}+1}=1-y\\
\iff&e{2x}+1=\dfrac1{1-y}\\
\iff&e{2x}=\dfrac1{1-y}-1=\dfrac{y}{1-y}\\
\iff&2x=\ln\lp\dfrac{y}{1-y}\rp\\
\iff&x=F^{-1}(y)=\dfrac12\ln\lp\dfrac{y}{1-y}\right)
\enar\]](/Generateur-Devoirs/Colles/VAC/ESCP-BL-2021-4.7_c/39.png)
- On a
Tag:Variables aléatoires continues
Autres sujets au hasard:

Voir aussi: