Lois de Pareto et exponentielle
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires continuesVariables aléatoires continues
Énoncé du sujet
Soit 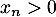 et soit
et soit 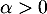 .
On définit
.
On définit 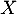 une variable aléatoire telle que:
une variable aléatoire telle que:
![\[\forall x\in\R, \ P(X>x)=\la\begin{array}{cl}\lp\dfrac{x_n}{x}\rp^\alpha &\text{si }\, x\geqslant x_n\\[1em]
1 &\text{sinon}\enar\right.\]](/Generateur-Devoirs/Colles/VAC/pareto-exp/4.png)
![\[\forall x\in\R, \ P(X>x)=\la\begin{array}{cl}\lp\dfrac{x_n}{x}\rp^\alpha &\text{si }\, x\geqslant x_n\\[1em]
1 &\text{sinon}\enar\right.\]](/Generateur-Devoirs/Colles/VAC/pareto-exp/4.png)
- Montrer que
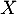 est une variable aléatoire à densité, calculer sa densité.
est une variable aléatoire à densité, calculer sa densité.
Représenter une allure de la fonction de répartition et de la densité.
On dit que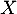 suit une loi de Pareto de paramètres
suit une loi de Pareto de paramètres 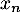 et
et 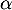 .
.
- Soit
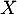 une variable aléatoire qui suit une loi de Pareto de paramètres
une variable aléatoire qui suit une loi de Pareto de paramètres 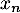 et
et 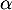 .
.
Calculer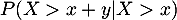 .
.
Qu'en est-il si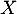 suit une loi exponentiellle de paramètre
suit une loi exponentiellle de paramètre  ?
?
- Montrer que :
![\[X \text{ est de loi de Pareto de param\`etres } x_n \text{ et } \alpha
\iff \ln\lp\dfrac{X}{x_n}\right) \text{ est de loi } \mathcal{E}(\alpha)\]](/Generateur-Devoirs/Colles/VAC/pareto-exp/15.png)
- À quelles conditions sur
 ,
,  admet-elle une espérance ?
admet-elle une espérance ?
Correction
Soit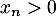 et soit
et soit 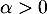 .
On définit
.
On définit 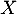 une variable aléatoire telle que:
une variable aléatoire telle que:
![\[\forall x\in\R, \ P(X>x)=\la\begin{array}{cl}\lp\dfrac{x_n}{x}\rp^\alpha &\text{si }\, x\geqslant x_n\\[1em]
1 &\text{sinon}\enar\right.\]](/Generateur-Devoirs/Colles/VAC/pareto-exp_c/4.png)
Correction
Oral ENSAE - Saclay - 2019Soit
![\[\forall x\in\R, \ P(X>x)=\la\begin{array}{cl}\lp\dfrac{x_n}{x}\rp^\alpha &\text{si }\, x\geqslant x_n\\[1em]
1 &\text{sinon}\enar\right.\]](/Generateur-Devoirs/Colles/VAC/pareto-exp_c/4.png)
- On note
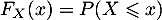 .
.
Alors, si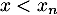 , on a
, on a 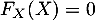 et pour
et pour  , on a
, on a
![\[F_X(x)=1-P(X>x)=1-\lp\dfrac{x_n}{x}\rp^\alpha\]](/Generateur-Devoirs/Colles/VAC/pareto-exp_c/9.png)
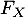 est continue sur
est continue sur 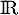 (à vérifier en
(à vérifier en 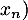 ,
et de classe
,
et de classe 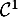 par morceaux, sauf en
par morceaux, sauf en 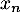 .
.
La fonction densité est alors
![\[f_X(x)=F'_X(x)=\la\begin{array}{cl}\alpha\dfrac{x_n^\alpha}{x^{\alpha+1}} &\text{si }\, x\geqslant x_n\\[1em]
1 &\text{sinon}\enar\right.\]](/Generateur-Devoirs/Colles/VAC/pareto-exp_c/15.png)
où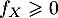 et
et
![\[\begin{array}{ll}\dsp\int_\R f_X(x)\,dx
&=\alpha x_n^\alpha\dsp\int_{x_n}^{+\infty}x^{-\alpha-1}dx\\
&=\alpha x_n^\alpha\left[ \dfrac1{-\alpha}x^{-\alpha}\rb_{x_n}^{+\infty}\\
&=1
\enar\]](/Generateur-Devoirs/Colles/VAC/pareto-exp_c/17.png)
et donc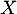 est bien une variable aléatoire à densité de densité
est bien une variable aléatoire à densité de densité 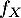 .
.
- Pour
 et donc
et donc 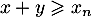 , on a
, on a
![\[\begin{array}{ll}P(X>x+y | X>x)&=\dfrac{P(X>x+y \cap X>x)}{P(X>x)}\\[1em]
&=\dfrac{P(X>x+y)}{P(X>x)}\\[1.2em]
&=\lp\dfrac{x}{x+y}\rp^\alpha
\enar\]](/Generateur-Devoirs/Colles/VAC/pareto-exp_c/22.png)
Si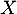 suit une loi exponentiellle de paramètre
suit une loi exponentiellle de paramètre 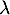 alors,
de même que précédemment,
alors,
de même que précédemment,
![\[\begin{array}{ll}P(X>x+y | X>x)&=\dfrac{P(X>x+y \cap X>x)}{P(X>x)}\\[1em]
&=\dfrac{P(X>x+y)}{P(X>x)}\\[1.2em]
&=\dfrac{e^{-\lambda(x+y)}}{e^{-\lambda x}}=e^{-\lambda y}=P(X>y)
\enar\]](/Generateur-Devoirs/Colles/VAC/pareto-exp_c/25.png)
- Soit la variable aléatoire
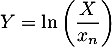 ,
alors par croissance du logarithme,
,
alors par croissance du logarithme,
![\[\begin{array}{ll}
P(Y\leqslant y)&=P\left( \ln\left(\dfrac{X}{x_n}\rp\leqslant y\rp\\[1em]
&=P\left( X\leqslant x_n e^y\rp\\[.6em]
&=\la\begin{array}{ll}
1-\lp\dfrac{x_n}{x_ne^y}\rp^\alpha &\text{ si } x_ne^y\geqslant x_n\\
0 & \text{ sinon }\enar\right.\\[2em]
&=\la\begin{array}{ll}
1-e^{-\alpha y} &\text{ si } y\geqslant 0\\
0 & \text{ sinon }\enar\right.\\
\enar\]](/Generateur-Devoirs/Colles/VAC/pareto-exp_c/27.png)
et on trouve bien que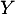 suit la loi
suit la loi 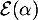 .
.
- On a
![\[\int_\R xf_X(x)\,dx=\alpha x_n^\alpha\int_{-\infty}^{+\infty}\dfrac1{x^\alpha}\,dx\]](/Generateur-Devoirs/Colles/VAC/pareto-exp_c/30.png)
Cette intégrale, de Riemann, converge, et donc l'espérance existe, si et seulement si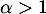 .
.
Tag:Variables aléatoires continues
Autres sujets au hasard:

Voir aussi: