Racine double et division euclidienne
Colle de mathématiques
Sujet de colle de maths:- PolynômePolynômes
Énoncé du sujet
Soit  .
.
- Déterminer
 tel que
tel que 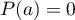 et
et  .
.
- Montrer qu'il existe
 et
et 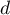 tels que
tels que
 . Déterminer
. Déterminer 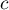 et
et  .
.
- Déterminer le reste de la division euclidienne de
 par
par  .
.
Correction
Correction
- On cherche donc une racine double de
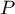 .
.
![\[\la\begin{array}{ll}
P(a)=0\iff a^3-4a^2+5a-2=0\\
P'(a)=0\iff 3a^2-8a+5=0
\enar\right.\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/2.png)
La deuxième équation est une équation du second degré qui a pour racines et
et 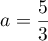 .
On vérifie facilement que
.
On vérifie facilement que  est aussi solution de la première équation
et nous donne donc la valeur recherchée.
est aussi solution de la première équation
et nous donne donc la valeur recherchée.
Remarque: en lisant l'ensemble des questions avant de commencer, on s'aperçoit qu'à la question 2 suivante, cette racine double est donnée ... (ce qui n'est bien sûr pas une démonstration)
-
 est donc une racine double du polynôme qui se factorise donc
par
est donc une racine double du polynôme qui se factorise donc
par  , soit
, soit
![\[P(X)=(X-1)^2Q(X)\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/8.png)
avec
![\[\deg(P)=\deg\lp(x-1)^2\rp+\deg(Q)\iff 3=2+\deg(Q)\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/9.png)
ce qui montre que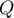 est un polynôme du premier degré, soit
est un polynôme du premier degré, soit
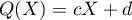 et donc
et donc
![\[P(X)=(X-1)^2(cX+d)\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/12.png)
En développant, on obtient
![\[\begin{array}{ll}P(X)&=\left( X^2-2X+1\rp(cX+d)\\
&=cX^3+(-2c+d)X^2+(c-2d)X+d\enar\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/13.png)
d'où il suffit d'avoir
![\[\la\begin{array}{rcr}
c&=&1\\
-2c+d&=&-4\\
c-2d&=&5\\
d&=&-2
\enar\right.
\iff\la\begin{array}{rcr}c&=&1\\d&=&-2\enar\right.\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/14.png)
et on a donc trouvé que
![\[P(X)=(X-1)^2(X-2)\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/15.png)
- On écrit la division euclidienne:
![\[X^n=P(X)Q_n(X)+R_n(X)\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/16.png)
avec le reste tel que
![\[\deg\left( R_n(X)\rp<\deg(P(X))=3\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/17.png)
d'où
![\[R_n(X)=a_nX^2+b_nX+c_n\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/18.png)
et donc
![\[X^n=P(X)Q_n(X)+a_nX^2+b_nX+c_n\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/19.png)
On détermine ensuite ces trois suites de coefficients:- Pour
 ,
on obtient
,
on obtient
![\[1^n=1=a_n+b_n+c_n\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/21.png)
- Pour
 , on obtient
, on obtient
![\[2^n=4a_n+2b_n+c_n\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/23.png)
- en dérivant,
![\[nX^{n-1 }=P'(X)Q(X)+P(X)Q'(X)+2a_nX+b_n\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/24.png)
et donc, vec qui est racine de
qui est racine de 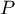 et
et 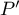 ,
,
![\[n1^{n-1}=n=2a_n+b_n\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/28.png)
![\[\mathcal{S} \la\begin{array}{rcrcrcl}
a_n&+&b_n&+&c_n&=&1\\
4a_n&+&2b_n&+&c_n&=&2^n\\
2a_n&+&b_n&&&=&n
\enar\right.\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/29.png)
Soit avec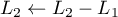
![\[\mathcal{S}\iff\la\begin{array}{rcrcrcl}
a_n&+&b_n&+&c_n&=&1\\
3a_n&+&b_n&&&=&2^n-1\\
2a_n&+&b_n&&&=&n
\enar\right.\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/31.png)
puis donne
donne
![\[a_n=2^n-n-1\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/33.png)
puis, en substituant
![\[b_n=n-2a_n=-2^{n+1}+3n+2\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/34.png)
et
![\[\begin{array}{ll}c_n&=1-a_n-b_n=2^{n+1}-2^n-2n\\
&=2^n\lp2-1\rp-2n=2^n-2n\enar\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP4_c/35.png)
- Pour
Tag:Polynôme
Autres sujets au hasard:

Voir aussi: