Projection du plan sur un cercle
Colle de mathématiques
Sujet de colle de maths:- ComplexesNombres complexs
Énoncé du sujet
Soit  le point d'affixe 1 du plan complexe.
On considère la transformation
le point d'affixe 1 du plan complexe.
On considère la transformation 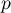 de plan complexe
qui à tout point
de plan complexe
qui à tout point 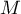 d'affixe
d'affixe 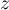 et distinct de
et distinct de 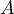 associe le point
associe le point 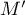 d'affixe
d'affixe 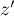 tel que
tel que
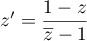 .
.
- Déterminer les antécédents de
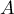 par la transformation
par la transformation 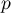 .
.
- Calculer le module de
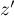 .
.
- Démontrer que les points
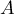 ,
, 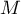 et
et 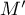 sont alignés.
sont alignés.
- En déduire une construction de
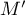 .
.
Correction
 le point d'affixe 1 du plan complexe.
On considère la transformation
le point d'affixe 1 du plan complexe.
On considère la transformation  de plan complexe
qui à tout point
de plan complexe
qui à tout point 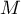 d'affixe
d'affixe 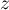 et distinct de
et distinct de 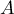 associe le point
associe le point 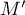 d'affixe
d'affixe  tel que
tel que
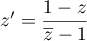 .
.
Correction
Soit-
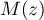 est un antécédent de
est un antécédent de 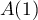 si
si
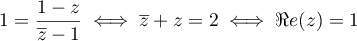 .
.
Il s'agit de la droite d'équation .
.
-
 .
.
-
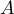 ,
, 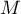 et
et 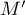 sont alignés si et seulement si
sont alignés si et seulement si
![\[\begin{array}{ll}
z-1=k(z'-1)$, $k\in\R$, soit
$z-1=k\left( \dfrac{1-z}{\overline{z}-1}-1\right)
=k\left( \dfrac{2-2\Re e(z)}{\overline{z}-1}\rp\\
\iff |z-1|^2=2k\lp1-\Re e(z)\right)
\enar\]](/Generateur-Devoirs/Colles/Complexes/ex13_c/17.png)
soit pour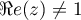 (les antécédents de
(les antécédents de 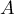 ),
),
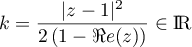 ,
et donc les points sont bien alignés.
,
et donc les points sont bien alignés.
Si avec
avec 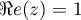 , alors
, alors  et les points sont aussi alignés.
et les points sont aussi alignés.
- Étant donné
 ,
, 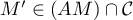 où
où 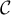 est le cercle unité.
est le cercle unité.
Tag:Complexes
Autres sujets au hasard:

Voir aussi: