Démonstration des inégalités triangulaires
Colle de mathématiques
Sujet de colle de maths:- ComplexesNombres complexs
Énoncé du sujet
Démontrer les inégalités triangulaires.
Correction
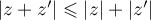 .
.
Soit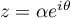 et
et 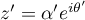 ,
avec
,
avec 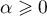 et
et
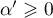 .
.
Alors,
![\[\begin{array}{ll}
|z+z'|^2=|\alpha e^{i\theta}+\alpha'e^{i\theta'}|^2
&=|e^{i\theta}|\,|\alpha+\alpha'e^{i(\theta'-\theta)}|^2\\
&=\lp\alpha+\alpha'\cos(\theta'-\theta)\rp^2
+\alpha'^2\sin^2(\theta'-\theta)\\
&=\alpha^2+\alpha'^2+2\alpha\alpha'\cos(\theta'-\theta)
\enar\]](/Generateur-Devoirs/Colles/Complexes/ex0_c/6.png)
car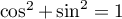 .
.
Comme de plus ,
on obtient
,
on obtient
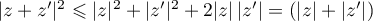 ,
et donc l'inégalité recherchée car tous les nombres sont positifs.
,
et donc l'inégalité recherchée car tous les nombres sont positifs.
Les cas d'égalité se déduisent aussi ici, lorsque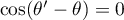 , soit lorsque
, soit lorsque ![$\theta'\equiv\theta\,[2\pi]$](/Generateur-Devoirs/Colles/Complexes/ex0_c/11.png) ,
soit lorsque
,
soit lorsque 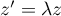 ,
, 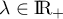 .
.
L'autre côté de l'inégalité s'obtient à partir de celle-ci appliquée à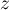 et
et 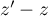 puis
à
puis
à 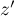 et
et 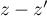 .
.
Correction
On démontre d'abordSoit
Alors,
![\[\begin{array}{ll}
|z+z'|^2=|\alpha e^{i\theta}+\alpha'e^{i\theta'}|^2
&=|e^{i\theta}|\,|\alpha+\alpha'e^{i(\theta'-\theta)}|^2\\
&=\lp\alpha+\alpha'\cos(\theta'-\theta)\rp^2
+\alpha'^2\sin^2(\theta'-\theta)\\
&=\alpha^2+\alpha'^2+2\alpha\alpha'\cos(\theta'-\theta)
\enar\]](/Generateur-Devoirs/Colles/Complexes/ex0_c/6.png)
car
Comme de plus
Les cas d'égalité se déduisent aussi ici, lorsque
L'autre côté de l'inégalité s'obtient à partir de celle-ci appliquée à
Tag:Complexes
Autres sujets au hasard:

Voir aussi: