Sous-espace vectoriel noyau d'une matrice et base de vecteurs
Colle de mathématiques
Sujet de colle de maths:- Espace vectorielEspaces vectoriels
- MatricesMatrices
Énoncé du sujet
Soit 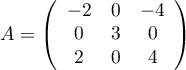 .
On pose
.
On pose 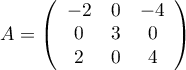 .
.
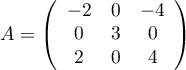 .
On pose
.
On pose 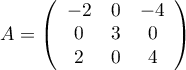 .
.
- Montrer que
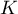 est un sous-espace vectoriel de
est un sous-espace vectoriel de 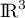 .
.
Donner un vecteur non nul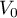 de
de 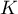 .
.
- On note
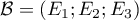 la base canonique de
la base canonique de 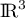 ,
et
,
et 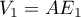 et
et 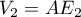 .
.
Montrer que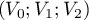 est une base de
est une base de 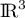 .
.
Correction
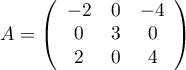 .
.
On pose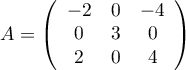 .
.
Correction
Soit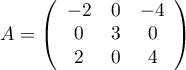 .
.
On pose
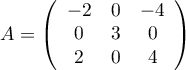 .
.
- Soit
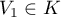 et
et 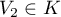 , et deux réels
, et deux réels 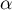 et
et 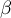 ,
alors
,
alors
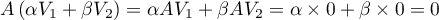 ,
et donc
,
et donc 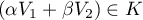 ,
ce qui montre que
,
ce qui montre que 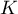 est un sous-espace vectoriel de
est un sous-espace vectoriel de 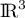 .
.
Soit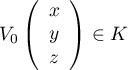 , alors
, alors
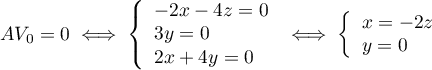
On peut donc choisir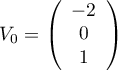 .
.
-
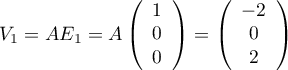 et
et 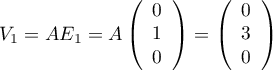
Pour montrer que est une base de
est une base de 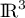 ,
il suffit de montrer que c'est une famille libre.
,
il suffit de montrer que c'est une famille libre.
Soit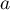 ,
,  et
et 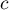 trois réels tels que
trois réels tels que
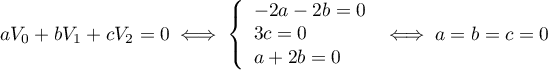 ,
ce qui montre que la famille est libre et est donc une base.
,
ce qui montre que la famille est libre et est donc une base.
Tags:Espace vectorielMatrices
Autres sujets au hasard:

Voir aussi: