projecteur dans le plan
Colle de mathématiques
Sujet de colle de maths:- ProjecteursProjecteurs dans des espaces vectoriels
- Applications linéairesApplications linéaires
Énoncé du sujet
L'application 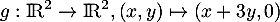 est-elle un projecteur ? Préciser ses éléments caractéristiques.
est-elle un projecteur ? Préciser ses éléments caractéristiques.
Correction
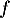 est tout d'abord une application linéaire puisque pour
est tout d'abord une application linéaire puisque pour 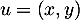 et
et 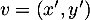 dans
dans 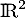 , et
, et 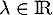 , on a
, on a 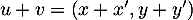 et:
et:
![\[\begin{array}{lcl}
f(u+v)&=&\bigr( (x+x')+3(y+y'), 0\bigl)\\[.4em]
&=&\big(x+3y+x'+3y', 0\bigr)\\[.4em]
&=&(x+3y,0)+(x'+3y', 0)\\[.4em]
&=&f(u)+f(v).
\enar\]](/Generateur-Devoirs/Colles/Applin/exPplan_c/7.png)
et avec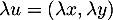 ,
,
![\[\begin{array}{lcl}
f(\lambda u)&=&(\lambda x+3\lambda y, 0)\\[.4em]
&=&\bigl(\lambda(x+3y),0\bigr)\\[.4em]
&=&\lambda(x+3y,0)\\[.4em]
&=&\lambda f(u).
\enar\]](/Generateur-Devoirs/Colles/Applin/exPplan_c/9.png)
Ainsi,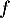 est un endomorphisme de
est un endomorphisme de 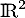 .
.
Un projecteur est caractérisé par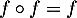 . Ici,
pour
. Ici,
pour 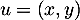 , on a
, on a 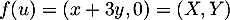 puis,
puis,
![\[\begin{array}{ll}f^2(u)&=f(f(u))=f(X,Y)\\[.3em]
&=f(X+3Y,0)\\[.3em]
&=\bigl((x+3y)+3\tm0,0\bigr)\\[.3em]
&=(x+3y,0)\\[.3em]
&=f(u)\enar\]](/Generateur-Devoirs/Colles/Applin/exPplan_c/15.png)
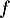 est donc bien un projecteur.
est donc bien un projecteur.
De plus,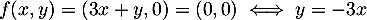 et donc, en posant
et donc, en posant 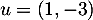
![\[\ker(f)=\text{Vect}(u)\]](/Generateur-Devoirs/Colles/Applin/exPplan_c/19.png)
L'image est simplement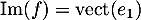 avec le vecteur
avec le vecteur 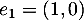 de la base canonique de
de la base canonique de 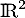 .
.
En résumé,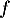 est un projecteur de
est un projecteur de 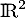 , projecteur sur
, projecteur sur 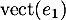 parallèlement à la droite
parallèlement à la droite 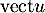 (d'équation
(d'équation 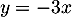 ).
).
Correction
![\[\begin{array}{lcl}
f(u+v)&=&\bigr( (x+x')+3(y+y'), 0\bigl)\\[.4em]
&=&\big(x+3y+x'+3y', 0\bigr)\\[.4em]
&=&(x+3y,0)+(x'+3y', 0)\\[.4em]
&=&f(u)+f(v).
\enar\]](/Generateur-Devoirs/Colles/Applin/exPplan_c/7.png)
et avec
![\[\begin{array}{lcl}
f(\lambda u)&=&(\lambda x+3\lambda y, 0)\\[.4em]
&=&\bigl(\lambda(x+3y),0\bigr)\\[.4em]
&=&\lambda(x+3y,0)\\[.4em]
&=&\lambda f(u).
\enar\]](/Generateur-Devoirs/Colles/Applin/exPplan_c/9.png)
Ainsi,
Un projecteur est caractérisé par
![\[\begin{array}{ll}f^2(u)&=f(f(u))=f(X,Y)\\[.3em]
&=f(X+3Y,0)\\[.3em]
&=\bigl((x+3y)+3\tm0,0\bigr)\\[.3em]
&=(x+3y,0)\\[.3em]
&=f(u)\enar\]](/Generateur-Devoirs/Colles/Applin/exPplan_c/15.png)
De plus,
L'image est simplement
En résumé,
Tags:ProjecteursApplications linéaires
Autres sujets au hasard:

Voir aussi: