Probabilité de naissances
Colle de mathématiques
Sujet de colle de maths:- Couples de variables aléatoiresCouples de variables aléatoires
Énoncé du sujet
On suppose que le nombre 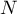 d'enfants dans une famille suit une loi de Poisson de paramètre
d'enfants dans une famille suit une loi de Poisson de paramètre  .
On suppose qu'à chaque naissance, la probabilité que l'enfant soit une fille
est
.
On suppose qu'à chaque naissance, la probabilité que l'enfant soit une fille
est ![$p\in ]0,1[$](/Generateur-Devoirs/Colles/CVA/Loi-naissance-filles-garcons/3.png) et celle que ce soit un garçon est
et celle que ce soit un garçon est 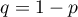 .
On suppose aussi que les sexes des naissances successives sont indépendants.
On note
.
On suppose aussi que les sexes des naissances successives sont indépendants.
On note  la variable aléatoire correspondant au nombre de filles par
familles, et
la variable aléatoire correspondant au nombre de filles par
familles, et  celle du nombre de garçons.
celle du nombre de garçons.
- Déterminer la loi conjointe du couple
 .
.
- En déduire la loi de
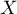 et celle de
et celle de 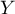 .
.
Correction
Correction
- Pour
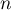 naissances, les lois de
naissances, les lois de 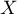 et
et 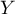 sont des lois binomiales de paramètres
sont des lois binomiales de paramètres 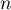 et respectivement
et respectivement  et
et 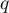 .
.
En d'autres termes, on a la probabilité conditionnelle
![\[P(X=k|N=n)=\left\{}\newcommand{\ra}{\right\}
\begin{array}{cll}\dsp\binom{n}{k}p^kq^{n-k}&\text{ si } k\leqslant n\\[1em]
0 &\text{ si } k>n\enar\right.\]](/Generateur-Devoirs/Colles/CVA/Loi-naissance-filles-garcons_c/7.png)
On en déduit que
![\[\begin{array}{ll}P(N=n,X=k)&=P(X=k|N=n)P(N=n)\\[.6em]
&=\la\begin{array}{cl}\dsp\binom{n}{k} p^k q^{n-k}e^{-\lambda}\frac{\lambda^n}{n!}&\text{ si } k\leqslant n\\[1em]
0&\text{ sinon}\enar\right.
\enar\]](/Generateur-Devoirs/Colles/CVA/Loi-naissance-filles-garcons_c/8.png)
- On déduit la loi marginale de
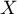 à partir de la loi du couple :
à partir de la loi du couple :
![\[\begin{array}{lcl}
P(X=k)&=&\dsp\sum_{n\geq k} P(X=k,N=n)\\
&=&\dsp\sum_{n\geq k}\frac{e^{-\lambda}\lambda^np^k q^{n-k}}{k!(n-k)!}\\[1.2em]
&=&\dfrac{e^{-\lambda}\lambda^k p^k}{k!}\dsp\sum_{n=k}^{+\infty}\dfrac{\lambda^{n-k}q^{n-k}}{(n-k)!}\\[1.2em]
&=&\dfrac{e^{-\lambda}\lambda^k p^k}{k!}\dsp\sum_{m=0}^{+\infty}\dfrac{\lambda^{m}q^{m}}{m!}\\[1.2em]
&=&\dfrac{e^{-\lambda}\lambda^k p^k}{k!}e^{\lambda q}\\[1em]
&=&\dfrac{e^{-\lambda p}(\lambda p)^k}{k!}
\enar\]](/Generateur-Devoirs/Colles/CVA/Loi-naissance-filles-garcons_c/10.png)
Ainsi, suit une loi de Poisson de paramètre
suit une loi de Poisson de paramètre  .
De même,
.
De même, 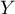 suit une loi de Poisson de paramètre
suit une loi de Poisson de paramètre 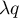 .
.
Tag:Couples de variables aléatoires
Autres sujets au hasard:
