Polynôme définissant par deux relations
Colle de mathématiques
Sujet de colle de maths:- PolynômePolynômes
Énoncé du sujet
Soit ![$P\in\R_5[X]$](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP6/1.png) tel que
tel que
![\[\la\begin{array}{ll}P(X)=(X+1)^3A(X)+4\\[.5em]
P(X)=12+(X-1)^3B(X)\enar\right.\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP6/2.png)
avec![$A(X)\in\R[X]$](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP6/3.png) et
et ![$B(X)\in\R[X]$](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP6/4.png) .
.
![\[\la\begin{array}{ll}P(X)=(X+1)^3A(X)+4\\[.5em]
P(X)=12+(X-1)^3B(X)\enar\right.\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP6/2.png)
avec
- Montrer que
 et
et 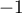 sont racines de
sont racines de 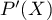 .
.
- Prouver que
 , avec
, avec 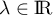 .
.
- En déduire que
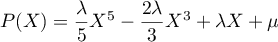 ,
avec
,
avec 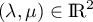 .
.
- Déterminer
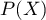 .
.
Correction
Correction
- En dérivant les relations définissant
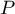 on obtient
on obtient
![\[\la\begin{array}{ll}P'(X)=3(X+1)^2A(X)+(X+1)^3A'(X)\\[.5em]
P'(X)=3(X-1)^2B(X)+(X-1)^3B'(X)\enar\right.\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP6_c/2.png)
d'où on trouve bien que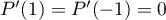 .
.
- Le résultat précédent montre aussi ue
 et
et 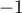 sont des racines doubles de
sont des racines doubles de 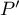 car
car
![\[\la\begin{array}{ll}P''(X)=6(X+1)A(X)+6(X+1)^2A'(X)+(X+1)^3A''(X)\\[.5em]
P''(X)=6(X-1)B(X)+6(X-1)^2B'(X)+(X-1)^3B''(X)\enar\right.\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP6_c/7.png)
et donc que aussi
![\[P''(1)=P''(-1)=0\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP6_c/8.png)
Ainsi,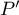 se factorise par
se factorise par  et
et 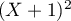 , soit
, soit
![\[\begin{array}{ll}P'(X)&=(X-1)^2(X+1)^2Q(X)\\
&=\lp(X-1)(X+1)\rp^2Q(X)\\
&=\left( X^2-1\rp^2Q(X)\enar\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP6_c/12.png)
Enfin, comme![$P\in\R_5[X]\iff \deg(P(X))=5$](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP6_c/13.png) , on a
, on a
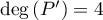 et comme
et comme 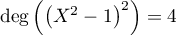 , on a nécessairement
, on a nécessairement
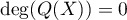 soit
soit 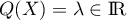 .
.
- En développant, on obtient
![\[P(X)=\lambda\left( X^2-1\rp^2
=\lambda X^4-2\lambda X^2+\lambda\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP6_c/18.png)
d'où les primitives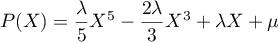 ,
avec
,
avec 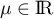 .
.
- En substituant cette expression précédente dans le système
définissant
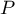 , et en utilisant les racines, on a
, et en utilisant les racines, on a
![\[\la\begin{array}{lcrcr}
P(-1)&=&4&=&-\dfrac\lambda5+\dfrac{2\lambda}3-\lambda +\mu\\[.7em]
P(1)&=&12&=&\dfrac\lambda5-\dfrac{2\lambda}3+\lambda+\mu\enar\right.\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP6_c/22.png)
En ajoutant ces deux équations, on obtient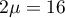 soit
soit 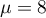 , puis en substituant cette valeur
on obtient
, puis en substituant cette valeur
on obtient
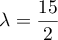 .
.
Tag:Polynôme
Autres sujets au hasard:

Voir aussi: