Parité des termes d'une suite et suite trigonométrique
Colle de mathématiques
Sujet de colle de maths:Énoncé du sujet
- Montrer que, pour tout entier
 ,
,
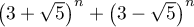 est un entier pair.
est un entier pair.
- En déduire que la suite
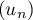 définie par
définie par
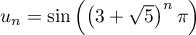 converge
et déterminer sa limite.
converge
et déterminer sa limite.
Correction
Correction
- À l'aide du binôme de Newton:
![\[\lp3+\sqrt5\rp^n+\lp3-\sqrt5\rp^n
=\sum_{k=0}^n \Cnp{n}{k}\left( 3^k\sqrt5^{n-k}+3^k\left(-\sqrt{5}\rp^{n-k}\rp
\]](/Generateur-Devoirs/Colles/Suites/exSPair_c/1.png)
Lorsque, dans la somme,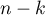 est impair,
on a
est impair,
on a 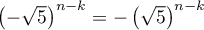 et le terme correspondant est nul,
tandis que si
et le terme correspondant est nul,
tandis que si 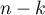 est impair, on a
est impair, on a
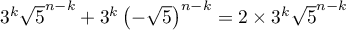 .
.
La somme est donc une somme de termes pairs et est donc paire.
On peut aussi démontrer cette propriété par récurrence. On a, initialement,
![\[u_0=\lp3+\sqrt5\rp^0+\lp3-\sqrt5\rp^0=2\]](/Generateur-Devoirs/Colles/Suites/exSPair_c/6.png)
et
![\[u_1=\lp3+\sqrt5\rp^1+\lp3-\sqrt5\rp^1=6\]](/Generateur-Devoirs/Colles/Suites/exSPair_c/7.png)
et donc ces deux premiers termes sont bien des entiers pairs.
L'hérédité est moins évidente. On doit faire intervenir l'expression de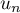 dans celle de
dans celle de 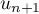 .
On peut "forcer" un peu les choses:
.
On peut "forcer" un peu les choses:
![\[\begin{array}{lcl}u_{n+1}&=&\lp3+\sqrt5\rp^{n+1}+\lp3-\sqrt5\rp^{n+1}\\[.6em]
&=&\Bigl[(3+\sqrt5)+(3-\sqrt5)\Bigr]\,\Bigl[(3+\sqrt5)^n+(3-\sqrt5)^n\Bigr]\\ [.4em]
&&-\Bigr[(3+\sqrt5)(3-\sqrt5)^n+(3-\sqrt5)(3+\sqrt5)^n\Bigr]\\[.5em]
&=&6u_n-(3+\sqrt5)(3-\sqrt5)\Bigl[(3-\sqrt5)^{n-1}+(3+\sqrt5)^{n-1}\Bigr]\\
&=&6u_n-4u_{n-1}
\enar\]](/Generateur-Devoirs/Colles/Suites/exSPair_c/10.png)
Il s'agit donc d'une démonstration par récurrence "à deux rangs": initialement la propriété est vraie aux rangs et
et  , puis
si on la suppose vraie aux rangs
, puis
si on la suppose vraie aux rangs 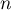 et
et 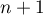 quelconques, c'est-à-dire que si
quelconques, c'est-à-dire que si 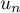 et
et 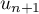 sont des entiers pairs,
alors le calcul précédent montre qu'au rang
sont des entiers pairs,
alors le calcul précédent montre qu'au rang 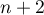
![\[u_{n+2}=2\lp3u_{n+1}-2u_n\rp\]](/Generateur-Devoirs/Colles/Suites/exSPair_c/18.png)
et la propriété est ainsi encore vraie.
Le principe de récurrence permet alors de conclure que la propriété est vraie pour tout entier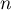 .
.
Remarque: on peut utiliser également une récurrence "forte": pour l'hérédité, on suppose que la propriété est vraie pour tout entier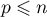 et on montre alors qu'elle encore vraie au rang
et on montre alors qu'elle encore vraie au rang 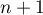 .
.
-
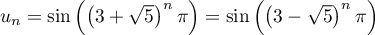 .
.
Or,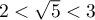 , et donc
, et donc 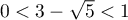 ,
et alors
,
et alors 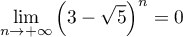 ,
et enfin,
,
et enfin, 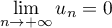 .
.
Tags:SuitesSommes
Autres sujets au hasard:

Voir aussi: