Paramètre pour un endomorphisme


Colle de mathématiques

Sujet de colle de maths:

Énoncé du sujet

On considère dans 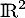$\R^2$ les trois vecteurs 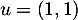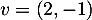$u=(1,1)$, $v=(2,-1)$ et $w=(1,4)$.
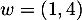  1. Démontrer que $(u,v)$ est une base de $\R^2$.
  2. Pour quelle(s) valeur(s) du réel $a$ existe-t-il une application linéaire $f:\R^2\to \R^2$ telle que
    $f(u)=(2,1)$, $f(v)=(1,-1)$ et $f(w)=(5,a)$ ?



Correction

Correction

  1. $(u,v)$ sont deux vecteurs non-nuls de $\R^2$, non colinéaires. Ils forment une famille libre de $\R^2$ de deux vecteurs. Or $\R^2$ est de dimension 2. $(u,v)$ est donc bien une base de $\R^2$.
  2. On cherche à utiliser la linéarité de $f$ pour exprimer $f(w)$ grâce à $f(u)$ et $f(v)$, et donc en exprimant directement $w$ grâce à $u$ et $v$ (ce qui est bien possible et même de manière unique car $(u,v)$ est une base).

    On cherche donc une combinaison linéaire $w=\alpha u+\beta v$. On écrit alors le système correspondant
    \[\la\begin{array}{lcl}1&=&\alpha+2\beta\\4&=&\alpha-\beta\enar\right.\]

    qui se résout en $\alpha=3$ et $\beta=-1$, et qui donne la relation linéaire $w=3u-v$.
    Pour que $f$ soit linéaire, on doit donc maintenant avoir
    \[f(w)=3f(u)-f(v)\]

    soit
    \[(5,a)=3(2,1)-(1,-1)=(5,4)\]

    Pour que $f$ soit linéaire, il est donc nécessaire que $a=4$.
    Réciproquement, on définit ainsi bien une application linéaire, en définissant l'image d'une base.


Tag:Applications linéaires

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0
Énoncé du sujet