Optimisation des dimensions d'une boite
Colle de mathématiques
Sujet de colle de maths:- Fonctions de plusieurs variablesFonctions de plusieurs variables
Énoncé du sujet
On désire fabriquer une boite ayant la forme d'un parallélépipède
rectangle, sans couvercle sur le dessus.
Le volume de cette boite doit être égal à 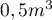 et
pour optimiser la quantité de matière utilisée, on désire que la somme
des aires des faces soit aussi petite que possible.
et
pour optimiser la quantité de matière utilisée, on désire que la somme
des aires des faces soit aussi petite que possible.
Quelles dimensions doit-on choisir pour fabriquer la boite?
Quelles dimensions doit-on choisir pour fabriquer la boite?
Correction
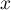 ,
, 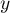 les dimensions de la base et
les dimensions de la base et 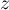 la hauteur de la boite.
Son volume est donc
la hauteur de la boite.
Son volume est donc 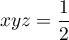 , et la somme des aires des faces,
sans couvercle, est
, et la somme des aires des faces,
sans couvercle, est
![\[f(x,y,z)=xy+2xz+2yz\]](/Generateur-Devoirs/Colles/FPV/optimisation-boite_c/5.png)
ou encore, en remplaçant ,
on cherche le minimum de la fonction de deux variables
,
on cherche le minimum de la fonction de deux variables
![\[g(x,y)=xy+\frac 1x+\frac 1y\]](/Generateur-Devoirs/Colles/FPV/optimisation-boite_c/7.png)
pour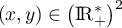 .
.
Les dérivées partielles de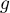 sont
sont
![\[\dfrac{\partial g}{\partial x}=y-\frac 1{x^2}
\text{ et }
\dfrac{\partial g}{\partial y}=x-\frac 1{y^2}\]](/Generateur-Devoirs/Colles/FPV/optimisation-boite_c/10.png)
Les points critiques sont solutions de
![\[\la\begin{array}{ll}y=\dfrac1{x^2}\\[.8em]
x=\dfrac1{y^2}
\enar\right.
\iff
\la\begin{array}{ll}y=y^4\\[.5em]
x=x^4
\enar\right.\]](/Generateur-Devoirs/Colles/FPV/optimisation-boite_c/11.png)
et le seul point critique de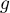 est
est 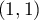 .
.
On calcule ensuite les dérivées secondes:
![\[\begin{array}{lcl}\dfrac{\partial^2 f}{\partial x^2}(x,y)&=&\dfrac2{x^3}
\\[1em]
\dfrac{\partial^2 f}{\partial y^2}(x,y)&=&\dfrac2{y^3}
\\[1em]
\dfrac{\partial^2 f}{\partial x\partial y}(x,y)&=&1
\enar\]](/Generateur-Devoirs/Colles/FPV/optimisation-boite_c/14.png)
et alors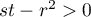 et
et
 admet donc un minimum en
admet donc un minimum en 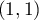 .
.
Les trois dimensions recherchées sont enfin ,
, 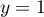 et
et 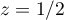 .
.
Correction
On noteou encore, en remplaçant
pour
Les dérivées partielles de
Les points critiques sont solutions de
![\[\la\begin{array}{ll}y=\dfrac1{x^2}\\[.8em]
x=\dfrac1{y^2}
\enar\right.
\iff
\la\begin{array}{ll}y=y^4\\[.5em]
x=x^4
\enar\right.\]](/Generateur-Devoirs/Colles/FPV/optimisation-boite_c/11.png)
et le seul point critique de
On calcule ensuite les dérivées secondes:
![\[\begin{array}{lcl}\dfrac{\partial^2 f}{\partial x^2}(x,y)&=&\dfrac2{x^3}
\\[1em]
\dfrac{\partial^2 f}{\partial y^2}(x,y)&=&\dfrac2{y^3}
\\[1em]
\dfrac{\partial^2 f}{\partial x\partial y}(x,y)&=&1
\enar\]](/Generateur-Devoirs/Colles/FPV/optimisation-boite_c/14.png)
et alors
Les trois dimensions recherchées sont enfin
Tag:Fonctions de plusieurs variables
Autres sujets au hasard:

Voir aussi: