Calcul des dérivées partielles

Colle de mathématiques

Sujet de colle de maths:

Calculer les dérivées partielles à l'ordre 2 de la fonction 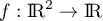$f:\R^2\to\R$ définie par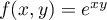 $f(x,y)=e^{xy}$

Correction

Les dérivées partielles premières sont

$\dfrac{\partial f}{\partial x}(x,y)=ye^{xy}$

$\dfrac{\partial f}{\partial y}(x,y)=xe^{xy}$

et les dérivées secondes

$\dfrac{\partial^2 f}{\partial x^2}(x,y)=y^2e^{xy}$

$\dfrac{\partial^2 f}{\partial y^2}(x,y)=x^2e^{xy}$

et enfin

$\dfrac{\partial^2 f}{\partial x\partial y}(x,y)=(1+xy)e^{xy}$

Autres sujets au hasard:

Voir aussi: