Nature de l'intégrale …
Colle de mathématiques
Sujet de colle de maths:- IntégraleIntégrale
Énoncé du sujet
Étudier la nature de l'intégrale
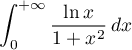
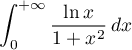
Correction
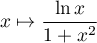 est continue sur
est continue sur ![$]0;+\infty[$](/Generateur-Devoirs/Colles/Integrale/exN7_c/2.png) et il suffit donc d'étudier la convergence de l'intégrale en
et il suffit donc d'étudier la convergence de l'intégrale en 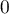 et en
et en 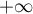 .
.
En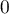 ,
, 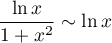 qui est intégrable (soit à l'aide
qui est intégrable (soit à l'aide 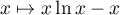 qui est une primitive de
qui est une primitive de  ,
soit car
,
soit car 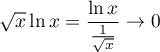 et donc
et donc 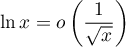 qui est le terme d'une intégrale de Riemann convergente en 0).
qui est le terme d'une intégrale de Riemann convergente en 0).
En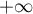 , par croissances comparées,
, par croissances comparées, 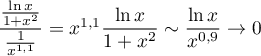 ce qui signifie que
ce qui signifie que
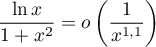 qui est le terme d'une intégrale de Riemann convergente.
qui est le terme d'une intégrale de Riemann convergente.
L'intégrale est donc convergente.
Correction
En
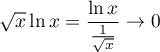 et donc
et donc En
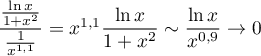 ce qui signifie que
ce qui signifie que
L'intégrale est donc convergente.
Tag:Intégrale
Autres sujets au hasard:

Voir aussi: