Maximum et maximum sur un carré
Colle de mathématiques
Sujet de colle de maths:- Fonctions de plusieurs variablesFonctions de plusieurs variables
Énoncé du sujet
- Déterminer les extrema de:
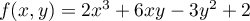 définie sur
définie sur 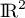
- Déterminer le maximum de
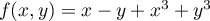 définie sur
définie sur ![$K=[0,1]\times[0,1]$](/Generateur-Devoirs/Colles/FPV/maximum-carre/4.png)
Correction
Correction
- On calcule les dérivées partielles de
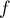 au premier ordre :
au premier ordre :
![\[\dfrac{\partial f}{\partial x}(x,y)=6x^2+6y
\text{ et }
\dfrac{\partial f}{\partial y}(x,y)=6x-6y\]](/Generateur-Devoirs/Colles/FPV/maximum-carre_c/2.png)
Un point critique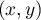 vérifie donc
vérifie donc
![\[\la\begin{array}{ll}
6x^2+6y=0\\
6x-6y=0\enar\right.
\iff
\la\begin{array}{ll}
x=y\\
x^2+x=x(x+1)=0
\enar\right.\]](/Generateur-Devoirs/Colles/FPV/maximum-carre_c/4.png)
et on trouve que les seuls points critiques sont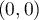 et
et 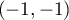 .
.
On calcule ensuite les dérivées au second ordre:
![\[\begin{array}{lcl}\dfrac{\partial^2 f}{\partial x^2}(x,y)&=&12x\\[1em]
\dfrac{\partial^2 f}{\partial y^2}(x,y)&=&-6\\[1em]
\dfrac{\partial^2 f}{\partial x\partial y}(x,y)&=&6
\enar\]](/Generateur-Devoirs/Colles/FPV/maximum-carre_c/7.png)
En , avec les notations usuelles,
, avec les notations usuelles,  ,
, 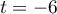 et
et  , soit
, soit 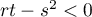 et donc
et donc 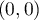 n'est pas un extrémum local pour
n'est pas un extrémum local pour 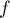 .
.
En , on a
, on a 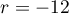 ,
, 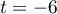 et
et  , soit
, soit 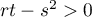 et
et  et donc
et donc 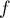 admet un maximum local en
admet un maximum local en  .
.
Ce maximum ne peut pas être un maximum global. En effet,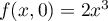 tend vers
tend vers 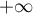 si
si  tend vers
tend vers 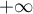 ,
et donc la fonction n'est pas majorée.
Par conséquent, elle n'admet pas de maximum global.
,
et donc la fonction n'est pas majorée.
Par conséquent, elle n'admet pas de maximum global.
- On a
![\[\frac{\partial f}{\partial x}(x,y)=1+3x^2>0\]](/Generateur-Devoirs/Colles/FPV/maximum-carre_c/27.png)
et donc ne peut pas admettre de point critique.
ne peut pas admettre de point critique.
On en déduit que le maximum de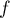 sur
sur 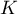 ne peut être atteint qu'en un point
du bord de
ne peut être atteint qu'en un point
du bord de 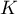 .
Il suffit ensuite d'étudier le comportement de
.
Il suffit ensuite d'étudier le comportement de 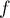 sur le bord de
sur le bord de  .
On a d'une part
.
On a d'une part 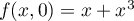 qui atteint son maximum en
qui atteint son maximum en 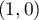 ,
maximum valant
,
maximum valant 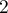 . On a ensuite
. On a ensuite 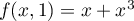 , qui atteint son maximum
valant 2 en
, qui atteint son maximum
valant 2 en  .
On a ensuite
.
On a ensuite  si
si ![$y\in[0,1]$](/Generateur-Devoirs/Colles/FPV/maximum-carre_c/40.png) , et
, et  .
Ainsi, le maximum de
.
Ainsi, le maximum de 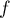 sur
sur  est égal à 2.
est égal à 2.
Tag:Fonctions de plusieurs variables
Autres sujets au hasard:

Voir aussi: