Fonction de deux variables sur un domaine borné
Colle de mathématiques
Sujet de colle de maths:- Fonctions de plusieurs variablesFonctions de plusieurs variables
Énoncé du sujet
Soit  et
et  .
On note de plus
.
On note de plus  le bord de
le bord de 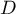 .
.
- Représenter
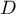 et
et  .
.
- Déterminer les points critiques de
 .
.
- Déterminer le minimum et le maximum de
 sur
sur  .
.
- En déduire le minimum et le maximum de
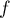 sur
sur  .
.
Correction
Correction
- Le domaine
 est délimité par les deux paraboles d'équation
est délimité par les deux paraboles d'équation 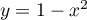 et
et  . Son bord
. Son bord  comporte deux parties:
la partie "haute", paramétrée par
comporte deux parties:
la partie "haute", paramétrée par  ,
,  , et la partie basse, paramétrée par
, et la partie basse, paramétrée par  ,
,  .
.
![\[\psset{unit=2cm,arrowsize=8pt}
\begin{pspicture}(-1.2,-1.2)(1.2,1.2)
\newcommand{\f}[1]{1 #1 2 exp sub}
\newcommand{\g}[1]{x 2 exp 1 sub}
\pscustom{
\psplot{-1}{1}{\f{x}} \gsave
\psplot{-1}{1}{\g{x}}
\fill[fillstyle=solid,fillcolor=lightgray]
\grestore
}
\psline{->}(-1.2,0)(1.3,0)
\psline{->}(0,-1.2)(0,1.3)
\psplot[linecolor=red,linewidth=1.8pt]{-1}{1}{\f{x}}
\psplot[linecolor=red,linewidth=1.8pt]{-1}{1}{\g{x}}
\rput(.8,.7){\red$\Gamma$}
\end{pspicture}\]](/Generateur-Devoirs/Colles/FPV/sur-un-domaine-borne_c/9.png)
- Pour déterminer les points critiques de
 , on calcule d'abord les dérivées partielles du premier ordre. On trouve :
, on calcule d'abord les dérivées partielles du premier ordre. On trouve :

Un point est un point critique si
est un point critique si 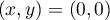 ou si
ou si 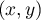 est solution du système
est solution du système
![\[\la\begin{array}{rcl}
1-y&=&0\\
2y&=&x^2.
\enar\right.\]](/Generateur-Devoirs/Colles/FPV/sur-un-domaine-borne_c/15.png)
On en déduit que admet trois points critiques qui sont
admet trois points critiques qui sont 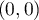 ,
,  et
et  .
.
 admet donc un seul point critique dans
admet donc un seul point critique dans 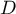 .
.
- Le bord
 est en deux parties, d'équations
est en deux parties, d'équations
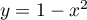 et
et 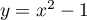 .
.
On étudie donc les valeurs prises par sur ce bord,
en posant
sur ce bord,
en posant  , pour
, pour ![$x\in[-1,1]$](/Generateur-Devoirs/Colles/FPV/sur-un-domaine-borne_c/27.png) et
et
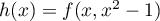 pour
pour ![$x\in [-1,1]$](/Generateur-Devoirs/Colles/FPV/sur-un-domaine-borne_c/29.png) .
.
On obtient, après simplifications,
![\[\begin{array}{lcl}
g(x)&=&1-2x^2+2x^4\\
h(x)&=&1.
\enar\]](/Generateur-Devoirs/Colles/FPV/sur-un-domaine-borne_c/30.png)
Il suffit donc d'étudier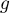 , et par parité, on peut se restreindre à l'étudier sur
, et par parité, on peut se restreindre à l'étudier sur ![$[0,1]$](/Generateur-Devoirs/Colles/FPV/sur-un-domaine-borne_c/32.png) . En calculant la dérivée, on voit facilement que
. En calculant la dérivée, on voit facilement que 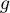 est décroissante sur
est décroissante sur
![$[0,1/\sqrt 2]$](/Generateur-Devoirs/Colles/FPV/sur-un-domaine-borne_c/34.png) et est croissante sur
et est croissante sur ![$[1/\sqrt 2,1]$](/Generateur-Devoirs/Colles/FPV/sur-un-domaine-borne_c/35.png) . De plus,
. De plus,  et
et 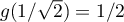 . On en déduit que le minimum de
. On en déduit que le minimum de  sur
sur 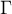 est
est  , et son maximum est
, et son maximum est  .
.
- Les extrema de
 sur
sur  sont ou bien atteints sur le bord, ou bien atteints en un extrémum local de
sont ou bien atteints sur le bord, ou bien atteints en un extrémum local de 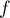 situé dans
situé dans  , donc en un point critique de
, donc en un point critique de  dans
dans  . Puisque
. Puisque  , on en déduit que
, on en déduit que  admet 0 comme minimum sur
admet 0 comme minimum sur  , et
, et  comme maximum.
comme maximum.
Tag:Fonctions de plusieurs variables
Autres sujets au hasard:

Voir aussi: