Matrices orthogonales, antisymétriques et valeurs propres
Colle de mathématiques
Sujet de colle de maths:- DiagonalisationDiagonalisation de matrice et réduction des endomorphismes
Énoncé du sujet
oral HEC, BL - 2022 - Sujet avec préparation
Soit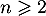 un entier.
Si
un entier.
Si 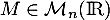 est une matrice, on note
est une matrice, on note 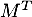 sa transposée.
sa transposée.
On dit qu'une matrice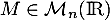 est orthogonale si
est orthogonale si 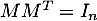 .
.
On dit qu'une matrice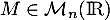 est symétrique si
est symétrique si 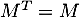 .
.
On dit qu'une matrice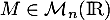 est antisymétrique si
est antisymétrique si 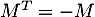 .
.
On confond dans la suite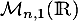 avec
avec 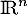 que l'on munit de son produit scalaire canonique noté
que l'on munit de son produit scalaire canonique noté 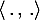 et de la norme associée notée
et de la norme associée notée  .
.
Soit
On dit qu'une matrice
On dit qu'une matrice
On dit qu'une matrice
On confond dans la suite
- Question de cours : rappeler la définition d'une matrice inversible.
-
- Montrer que toute matrice orthogonale est inversible.
- Soit
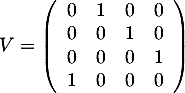 .
Préciser pour quelle(s) valeur(s) de
.
Préciser pour quelle(s) valeur(s) de 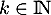 , la matrice
, la matrice 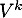 est orthogonale.
est orthogonale.
- Soit
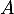 une matrice antisymétrique de
une matrice antisymétrique de 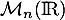 .
Soit
.
Soit 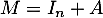 et
et 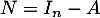 .
.
- Soit
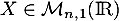 . Calculer
. Calculer 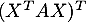 et en déduire la valeur de
et en déduire la valeur de 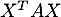 .
.
- Montrer que la seule valeur propre possible pour
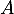 est 0.
Dans quel cas la matrice
est 0.
Dans quel cas la matrice 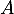 est-elle diagonalisable ?
est-elle diagonalisable ?
- Montrer que les matrices
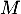 et
et 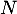 sont inversibles.
sont inversibles.
- Montrer que les matrices
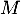 et
et 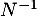 commutent.
commutent.
- Montrer que la matrice
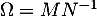 est orthogonale.
est orthogonale.
-
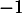 est-il valeur propre de
est-il valeur propre de 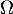 ?
?
- Soit
- Soit
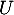 une matrice orthogonale de
une matrice orthogonale de 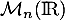 n'admettant pas
n'admettant pas 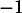 comme valeur propre. Montrer qu'il existe une unique matrice antisymétrique
comme valeur propre. Montrer qu'il existe une unique matrice antisymétrique 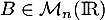 telle que
telle que
![\[U=(I_n+B)(I_n-B)^{-1}\]](/Generateur-Devoirs/Colles/Diagonalisation/HEC-BL-2022-1.1/37.png)
Correction
Correction
oral HEC, BL - 2022- Une matrice
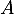 carrée d'ordre
carrée d'ordre 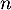 est inversible si et seulement il existe une matrice
est inversible si et seulement il existe une matrice 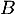 telle que
telle que 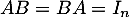 .
.
Dans ce cas, cette matrice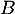 est l'inverse de
est l'inverse de 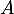 , notée
, notée 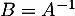 .
.
On sait de plus, qu'il suffit d'avoir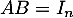 pour en déduire qu'aussi
pour en déduire qu'aussi 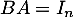 .
.
-
- D'après le rappel précédent, une matrice
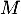 orthogonale vérifie bien le critère précédent, avec comme matrice inverse
orthogonale vérifie bien le critère précédent, avec comme matrice inverse  .
.
- On a
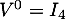 qui est bien orthogonale, puique
qui est bien orthogonale, puique 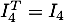 et donc
et donc
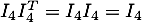 .
.
On calcule ensuite que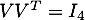 et donc que
et donc que 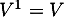 est orthogonale.
est orthogonale.
On en déduit que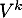 est orthogonale pour tout entier
est orthogonale pour tout entier 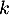 , puisque en regroupant successivement les termes centraux on a grâce au calcul précédent
, puisque en regroupant successivement les termes centraux on a grâce au calcul précédent
![\[\begin{array}{ll}V^k\left( V^k\rp^T&= VV\dots V V^T\dots V^T\\
&= VV\dots V(VV^T)V^T\dots V^T\\
&= VV\dots V(I_4)V^T\dots V^T\\
&=\dots\\
&= V(I_4)V^T\\
&=I_4
\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/HEC-BL-2022-1.1_c/19.png)
- D'après le rappel précédent, une matrice
-
- Comme
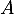 est antisymétrique, on a
est antisymétrique, on a
![\[(X^TAX)^T=X^TA^T(X^T)^T=-X^TAX\]](/Generateur-Devoirs/Colles/Diagonalisation/HEC-BL-2022-1.1_c/21.png)
et d'autre part, puisque, en regardant les dimensions de ce produit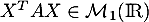 , c'est-à-dire que
, c'est-à-dire que 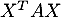 est un réel (une matrice à une seule ligne et une seule colonne), on a donc que
est un réel (une matrice à une seule ligne et une seule colonne), on a donc que
![\[(X^TAX)^T=X^TAX\]](/Generateur-Devoirs/Colles/Diagonalisation/HEC-BL-2022-1.1_c/24.png)
On déduit de ces deux expressions que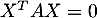 .
.
- Soit
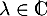 une éventuelle valeur propre de
une éventuelle valeur propre de 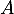 , et soit alors
, et soit alors 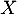 un vecteur propre associé, en d'autres termes
un vecteur propre associé, en d'autres termes
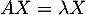 et on a alors, d'après la question précédente,
et on a alors, d'après la question précédente,
![\[0=X^TAX=X^T(\lambda X) = \lambda X^TX=\lambda \|X\|^2\]](/Generateur-Devoirs/Colles/Diagonalisation/HEC-BL-2022-1.1_c/30.png)
Si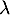 est valeur propre, c'est qu'il existe un tel vecteur propre non nul, et donc que, nécessairement
est valeur propre, c'est qu'il existe un tel vecteur propre non nul, et donc que, nécessairement 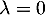 .
.
La seule valeur propre possible pour une matrice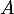 antisymétrique est donc bien 0.
antisymétrique est donc bien 0.
Une telle matrice n'est donc pas diagonalisable, car si elle l'était, avec 0 pour seule valeur propre, elle serait semblable à la matrice nulle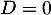 :
:
![\[A=PDP^1=0\]](/Generateur-Devoirs/Colles/Diagonalisation/HEC-BL-2022-1.1_c/35.png)
La seule matrice antisymétrique diagonalisable est donc la matrice nulle.
- On peut s'intéresser au noyau de
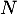 :
:
![\[NX=0\iff (I_n-A)X=0\iff AX=X\]](/Generateur-Devoirs/Colles/Diagonalisation/HEC-BL-2022-1.1_c/37.png)
Or 1 n'est pas valeur propre de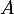 (la seule possible est 0), donc nécessairement
(la seule possible est 0), donc nécessairement 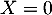 ce qui montre que
ce qui montre que 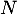 est inversible (l'endomorphisme associé est injectif, donc bijectif).
est inversible (l'endomorphisme associé est injectif, donc bijectif).
De même pour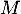 , car, comme précédemment,
, car, comme précédemment, 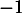 n'est pas valeur propre non plus de
n'est pas valeur propre non plus de 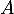 .
.
- Comme
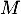 et
et 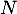 commutent (car
commutent (car 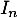 et
et 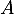 commutent),
on a alors
commutent),
on a alors
![\[\begin{array}{ll}
MN^{-1}&=(N^{-1}N)MN^{-1}\\
&=N^{-1}(NM)N^{-1}\\
&=N^{-1}(MN)N^{-1}\\
&=N^{-1}M(NN^{-1})\\
&=N^{-1}M
\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/HEC-BL-2022-1.1_c/48.png)
- On a tout d'abord, puisqu'on va s'intéresser aux transposées, et comme
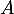 est antisymétrique
est antisymétrique
![\[M^T=(I_n+A)^T=I_n+A^T=I_n-A=N\]](/Generateur-Devoirs/Colles/Diagonalisation/HEC-BL-2022-1.1_c/50.png)
et
![\[N^T=(I_n-A)^T=I_n-A^T=I_n+A=M\]](/Generateur-Devoirs/Colles/Diagonalisation/HEC-BL-2022-1.1_c/51.png)
et alors, en revenant à la matrice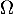 ,
,
![\[\begin{array}{ll}\Omega^T\Omega&=(MN^{-1})^T(MN^{-1})\\
&= (N^{-1})^TM^TMN^{-1}\\
&= M^{-1}NMN^{-1}
\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/HEC-BL-2022-1.1_c/53.png)
et comme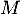 et
et 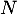 commutent,
commutent,
![\[\Omega^T\Omega=I_n\]](/Generateur-Devoirs/Colles/Diagonalisation/HEC-BL-2022-1.1_c/56.png)
c'est-à-dire que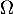 est une matrice orthogonale.
est une matrice orthogonale.
- Soit
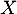 tel que
tel que 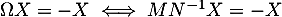 puis, comme
puis, comme 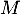 et
et 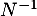 commutent, on a alors
commutent, on a alors
![\[\begin{array}{ll}N^{-1}MX=-X
&\iff MX=-NX\\
&\iff (I_n+A)X=-(I_n-A)X\\
&\iff 2X=0\\
&\iff X=0\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/HEC-BL-2022-1.1_c/62.png)
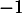 ne peut donc pas être valeur propre de
ne peut donc pas être valeur propre de 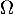 .
.
- Comme
- Suppsosns qu'une telle matrice
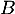 existe telle que
existe telle que
![\[\begin{array}{ll}U=(I_n+B)(I_n-B)^{-1}\\
&\iff U(I_n-B)=(I_n+B)\\
&\iff U-UB=I_n+B\\
&\iff (I_n+U)B=U-I_n\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/HEC-BL-2022-1.1_c/66.png)
et comme on l'a montré précédemment,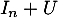 est inversible car
est inversible car 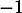 n'est pas valeur propre de
n'est pas valeur propre de 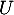 , d'où on trouve l'expression nécessaire de cette unique matrice
, d'où on trouve l'expression nécessaire de cette unique matrice 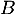 , si elle existe.
, si elle existe.
![\[B=(U+I_n)^{-1}(U-I_n)\]](/Generateur-Devoirs/Colles/Diagonalisation/HEC-BL-2022-1.1_c/71.png)
Réciproquement, si on définit la matrice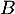 par l'expression précédente, on montre que
par l'expression précédente, on montre que 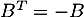 c'est-à-dire que
c'est-à-dire que 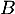 est antisymétrique et telle que, en reprenant le calcul précédant dans l'autre sens,
est antisymétrique et telle que, en reprenant le calcul précédant dans l'autre sens,
![\[U=(I_n+B)(I_n-B)^{-1}\]](/Generateur-Devoirs/Colles/Diagonalisation/HEC-BL-2022-1.1_c/75.png)
c'est-à-dire que la matrice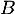 ainsi définie est bien l'unique matrice répondant à la question.
ainsi définie est bien l'unique matrice répondant à la question.
Tag:Diagonalisation
Autres sujets au hasard:
