Rang et diagonalisabilité d'une matrice nilpotente d'indice 2

Colle de mathématiques

Sujet de colle de maths:

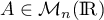Soit $A\in\mathcal{M}_n(\R)$ une matrice non nulle et nilpotente d'indice 2, c'est-à-dire telle que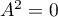

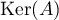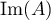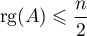Donner une relation d'inclusion entre $\text{Ker}(A)$ et $\text{Im}(A)$ et en déduire que $\text{rg}(A)\leqslant\dfrac{n}2$ .
Quelles sont les valeurs propres de 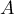? 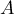est-elle diagonalisable ?

Correction

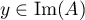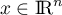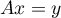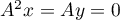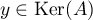Soit $y\in\text{Im}(A)$ , alors il existe $x\in\R^n$ tel que et donc , d'où $y\in\text{Ker}(A)$ .
On vient ainsi de montrer que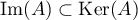 $\text{Im}(A)\subset\text{Ker}(A)$ .

On en déduit en particulier que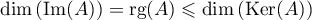 $\text{dim}\lp\text{Im}(A)\rp=\text{rg}(A) \leqslant\text{dim}\lp\text{Ker}(A)\rp$ . Le théorème du rang nous donne par ailleurs que $\text{rg}(A)+\text{dim}\lp\text{Ker}(A)\rp=n$
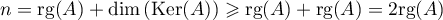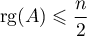et donc $n=\text{rg}(A)+\text{dim}\lp\text{Ker}(A)\right) \geqslant\text{rg}(A)+\text{rg}(A)=2\text{rg}(A)$ . On en déduit donc que $\text{rg}(A)\leqslant\dfrac{n}2$ .
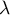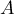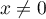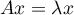Soit $\lambda$ une valeur propre de . Il existe alors $x\in\R^n$ , $x\not=0$ , tel que $Ax=\lambda x$ .
On obtient alors que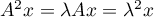 $A^2x=\lambda Ax=\lambda^2x$ et donc que 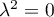$\lambda^2=0$ , soit 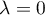$\lambda=0$ : la seule valeur propre possible pour 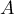est .

Si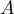 était diagonalisable, serait semblable à la matrice nulle (la matrice diagonale avec que des valeurs nulles dans la diagonale...), et donc serait nulle, ce qui n'est pas le cas.
n'est donc as diagonalisable.

Autres sujets au hasard:

Voir aussi: