Matrice inversible ? diagonalisable ?
Colle de mathématiques
Sujet de colle de maths:- DiagonalisationDiagonalisation de matrice et réduction des endomorphismes
- MatricesMatrices
Énoncé du sujet
La matrice 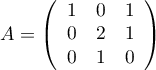 est-elle inversible ? diagonalisable ?
est-elle inversible ? diagonalisable ?
 est-elle inversible ? diagonalisable ?
est-elle inversible ? diagonalisable ?
Correction
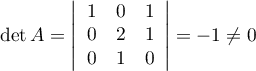 donc
donc 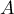 est inversible.
est inversible.
Le polynôme caractéristique de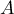 est:
est:
![\[\begin{array}{ll}
\chi_A(X)=\det\left( A-XI_3\right)
&=\left|\begin{array}{ccc} 1-X&0&1\\0&2-X&1\\0&1&-X\enar\right| \\
&=(1-X)\Bigl(-X(2-X)-1\Bigr)\\[.5em]
&=(1-X)\left( X^2-2X-1\right)
\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/ex01_c/4.png)
or le trinôme du second degré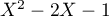 admet pour discriminant
admet pour discriminant
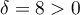 et donc admet deux racines rélles distinctes.
et donc admet deux racines rélles distinctes.
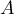 est donc diagonalisable.
est donc diagonalisable.
Correction
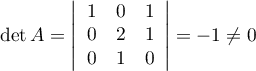 donc
donc Le polynôme caractéristique de
![\[\begin{array}{ll}
\chi_A(X)=\det\left( A-XI_3\right)
&=\left|\begin{array}{ccc} 1-X&0&1\\0&2-X&1\\0&1&-X\enar\right| \\
&=(1-X)\Bigl(-X(2-X)-1\Bigr)\\[.5em]
&=(1-X)\left( X^2-2X-1\right)
\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/ex01_c/4.png)
or le trinôme du second degré
Tags:DiagonalisationMatrices
Autres sujets au hasard:

Voir aussi: